摘要:数据结构中,线性结构有数组、字符串、链表,栈和队列、哈希表,非线性结构有堆、树、二叉树、图。
目录
[TOC]
数据结构
线性数据结构:数组(字符串)、链表、栈和队列、哈希表;
非线性结构有:堆、树、二叉树、图。
数组
顺序表,支持随机访问。
1 | |
nSum
nSum:取出数组中 n 个数, 相加之和为 target。
- 1.两数之和 无序数组:用
HashMap<nums[i], i>。注意return new int[]{i, j}; return new int[0];;也可用HashMap<target - nums[i], i>。

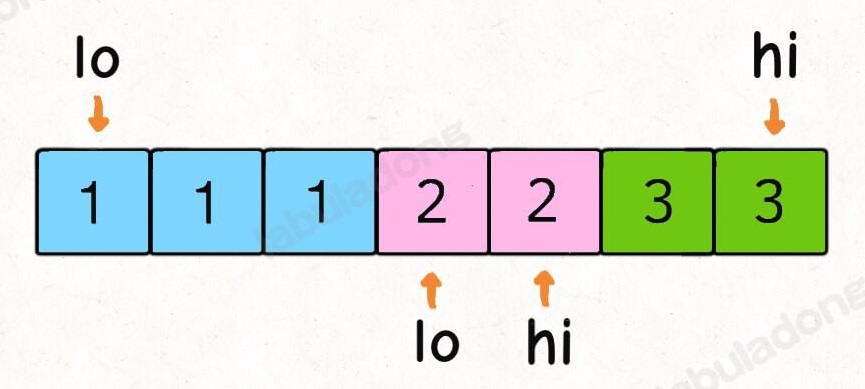
- 167.两数之和 II - 有序数组:两数之和为
target的所有元素对,结果不能出现重复。思路就是交换排序 + 双指针,sum = nums[lo] + nums[hi], 若sum > target 则hi--, 若sum < target 则lo++;注意跳过重复元素对。

- 15.三数之和:nSum框架 = 递归 + 2Sum,
List<List<Integer> > nSubSum = nSum(nums, n-1, i+1, target-nums[i]);表示从i+1位置开始求(n-1)Sum,加上nums[i]即为nSum的结果。
前缀和
前缀和技巧:preSum[i] = sum(nums[0, ..., i-1]),表示前 i-1 项的累加和。
主要用于:快速计算一个区间内的元素和。
主要适用场景是:不修改原始数组的情况下,频繁查询某区间的累加和。时间复杂度降为 O(1)。
1 | |
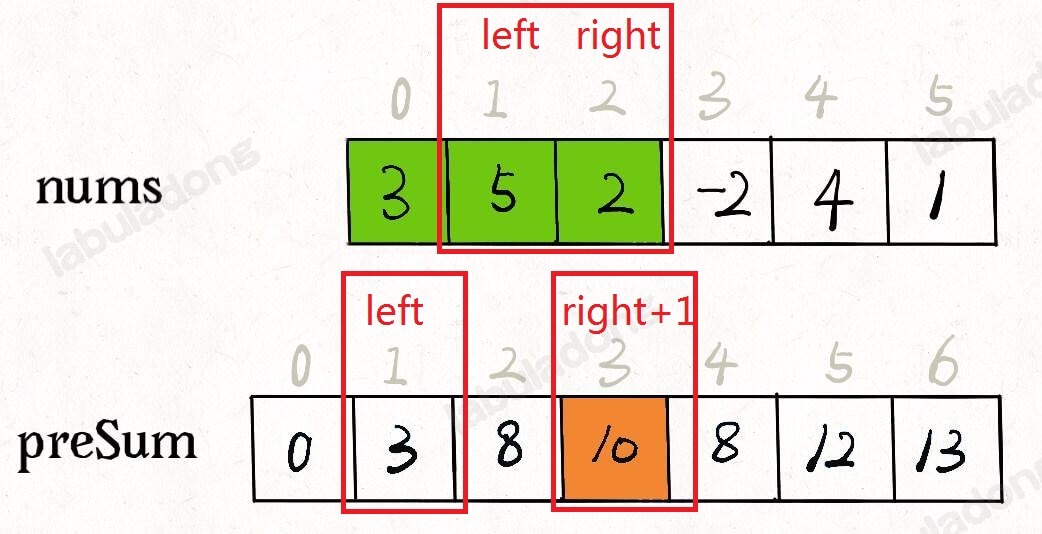
- 303.sumRange 区域和 - 数组不可变:对
nums[left, ..., right]求和,即preSums[left+1, ..., right+1],通过preSums[right+1] - preSums[left]。
- 304.二维区域和 - 矩阵不可变:
preSum[0][0] = 0;preSum[i+1][j+1]记录matrix中的子矩阵[1, 1, i, j]的元素累加和,i, j > 0。
差分数组
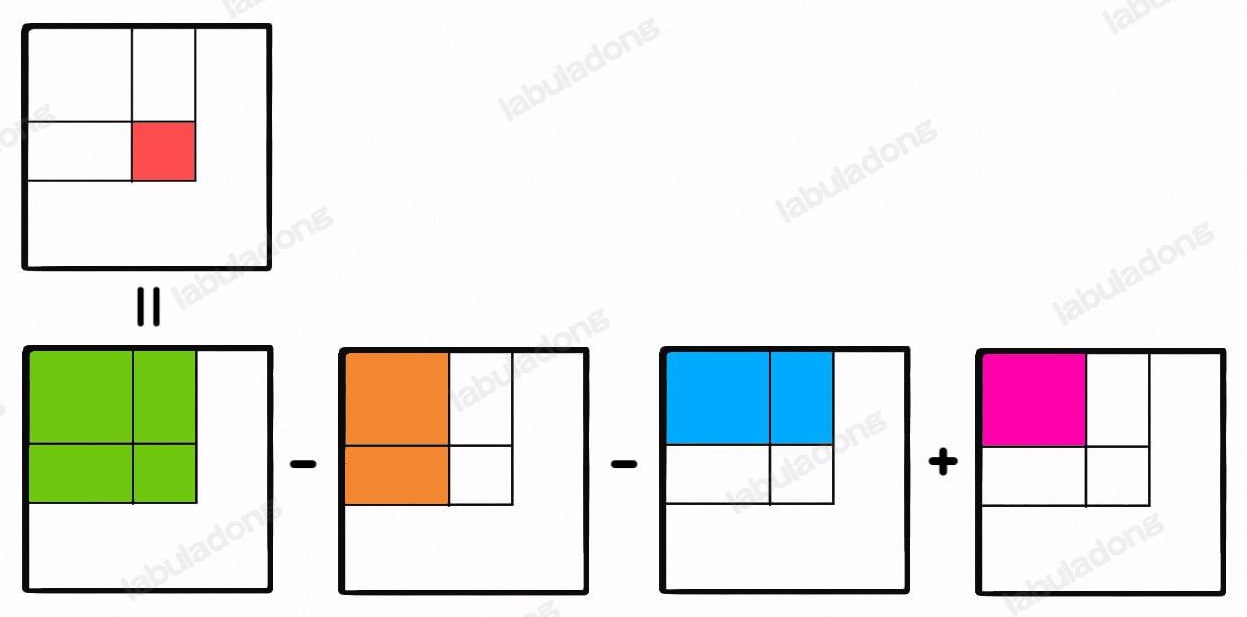
差分数组主要适用场景是:频繁对原始数组某区间的元素值进行增减。类似环比。
主要用于:快速修改整个区间的元素。
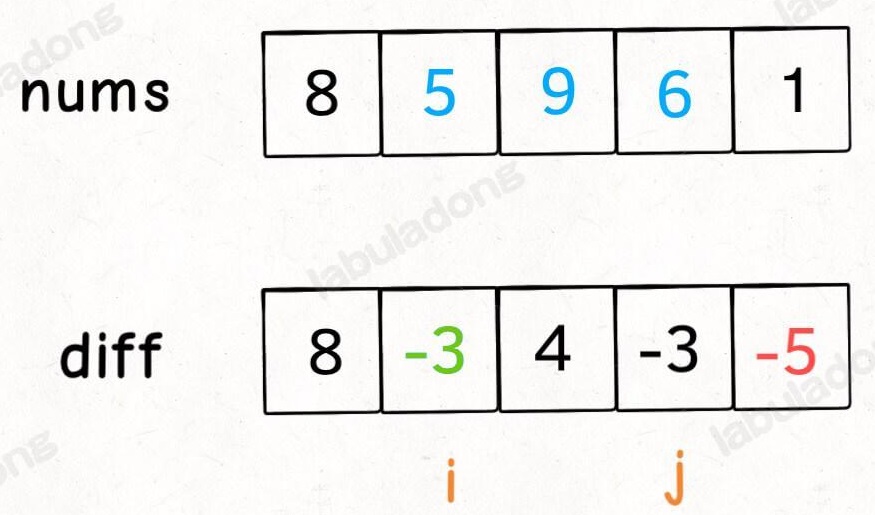
diff 数组:diff[0] = nums[0],diff[i] = nums[i] - nums[i-1],表示相邻元素间的差值。
- 恢复到原数组:
nums[i] = nums[i-1] + diff[i]。 - 对区间
nums[i..j]的元素全部加 3,只需让diff[i] += 3,再让diff[j+1] -= 3即可。
有序数组
见二分查找
二维数组的花式遍历
- 剑指 Offer 04.二维递增数组中二分查找:从左下角开始遍历,比
target大则向上row--,小则向右col++;用二分查找效率低。类似二叉查找树。 - 54.矩阵的螺旋遍历、剑指 Offer 29. 顺时针打印矩阵:收缩四个边界
- 48.顺时针旋转 90 度图像:沿对角线反转矩阵,再反转每一行。【】
双指针
头尾对向双指针
前后相向双指针、左右指针
- 见 nSum
- 见 判断全串是否回文
- 344.原地反转字符数组 O(1) 额外空间:数组,双指针 swap()
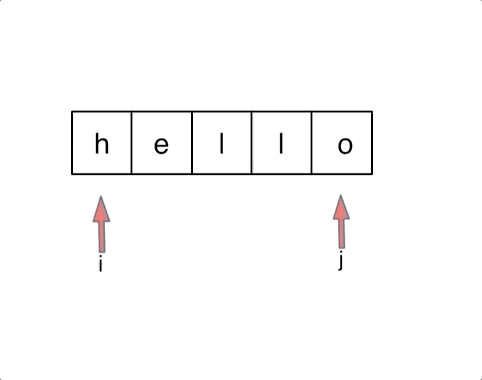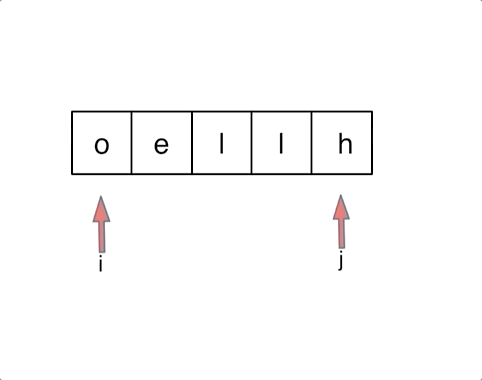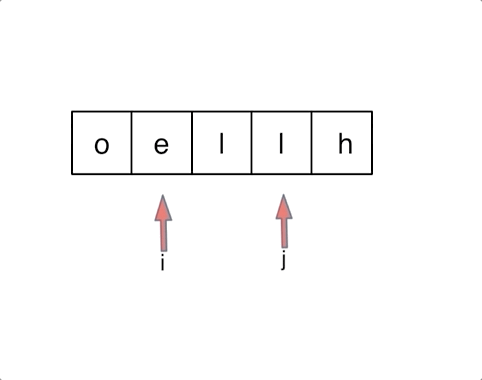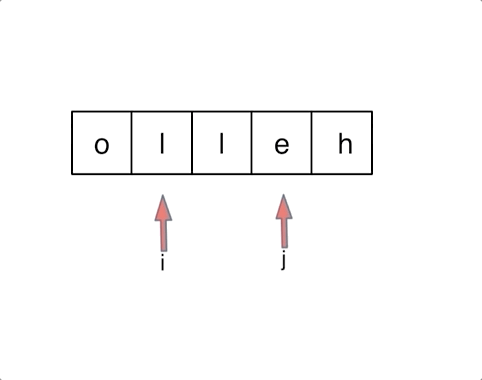
- 剑指 Offer 21.调整数组顺序使奇数位于前半部分:头指针指向第一个偶数,尾指针指向倒数第一个奇数;
while(l < r)。
背向双指针
- 基本上都是回文串,见 获取最长回文子串内容
同向双指针
- 88.合并两个有序数组:拉链法,将双指针初始化在数组的尾部,从后向前合并合并到 a1 中,因此不需要新 new 数组,可避免占用多余空间;开始时 a1 的长度即为
m + n。用于归并排序。
快慢双指针
-
234.判断回文链表 :找链表中点,见回文链表、链表快慢双指针
-
快慢指针指向的元素值相等时,就后移快指针;fast = 1;快指针与慢指针值不同时,将快指针的值附到慢指针后if(nums[slow] != nums[fast]) nums[++slow] = nums[fast](与第一种方法思想不同,实现代码类似)。slow指向结果数组的最后一项,fast指向(后续数组中)不重复的第一项,故要先++slow。
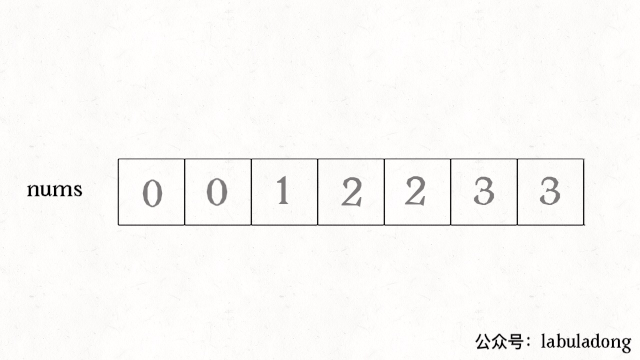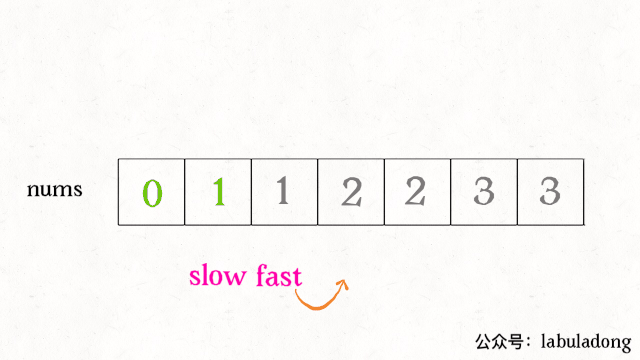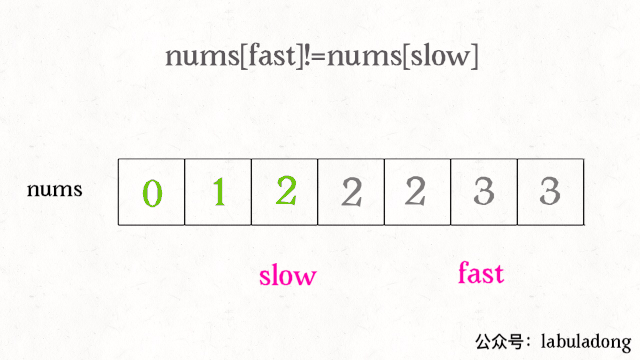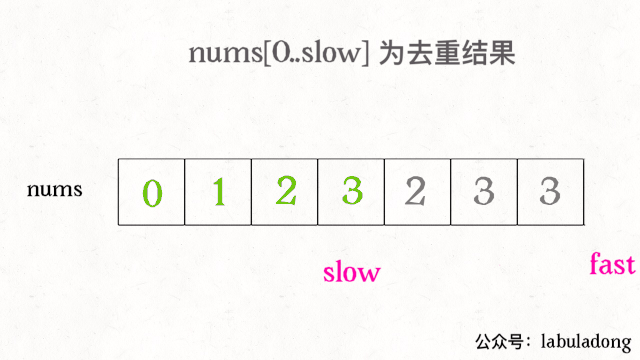
-
27.原地移除元素:不需单调数组,快指针不为某值时覆盖慢指针。
fast = 0; if(nums[i] != val) nums[slow++] = nums[fast];- 283.原地移动零:复用 [27.原地移除元素] 的解法移除所有 0
int p = removeElement(nums, 0),返回p为移除 0 之后的数组长度;把 p 及其后元素都置为 0,即相当于移动所有 0 到最后。【】

- 283.原地移动零:复用 [27.原地移除元素] 的解法移除所有 0
数组处理滑动窗口
见下字符串中。
二分搜索
经典例题
- 118.杨辉三角:二维 List,输入上一层的元素,生成并返回下一层的元素【】
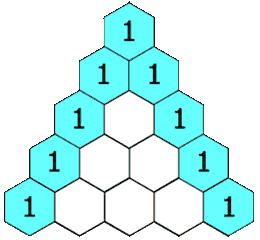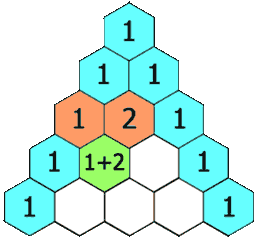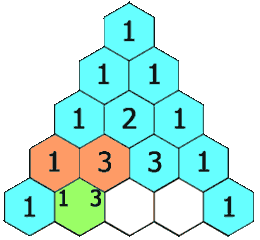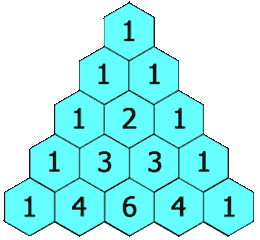
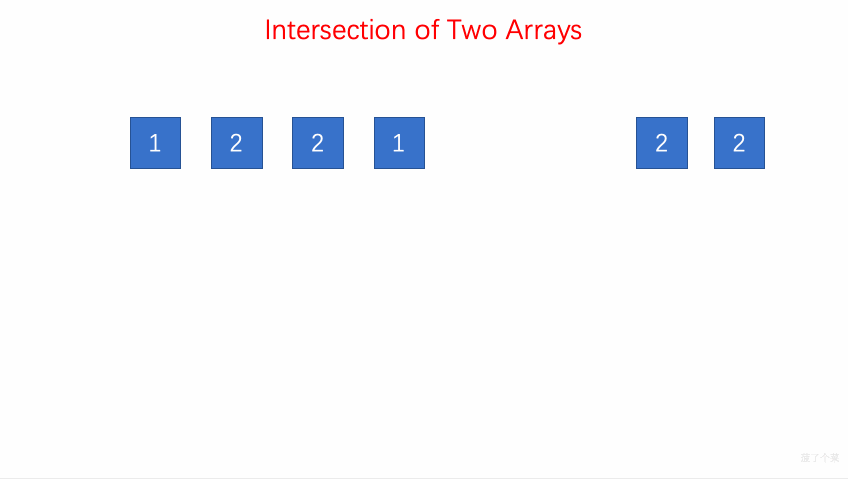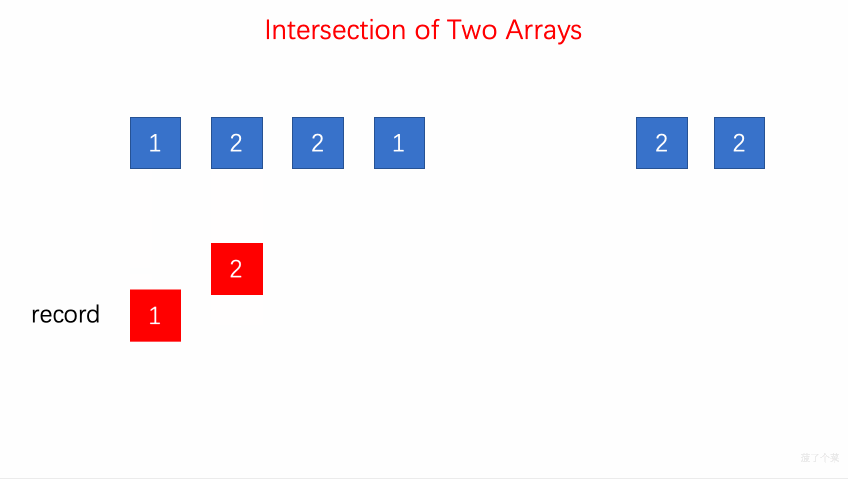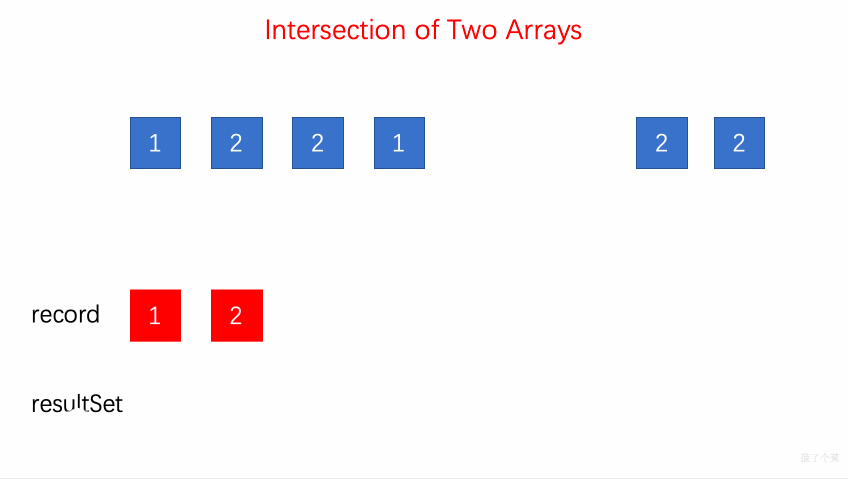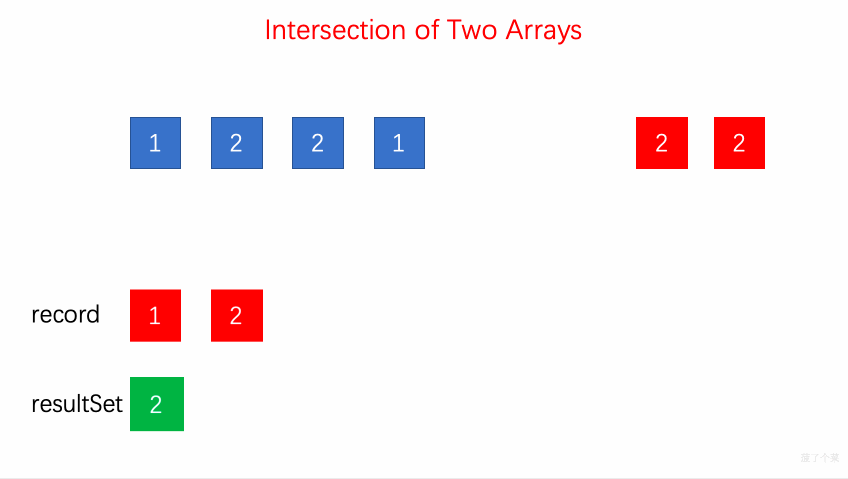
- 349.两个数组的交集:
insertset 容器record存储a1的元素,遍历a2find查找是否有相同的元素,如果有,用 set 容器resultSet进行存储,用iterator将 resultSet 转换为 vector 类型。【】

字符串
Java 对字符串的处理较麻烦,见常见类 String 类的常用方法。
回文串
方法一、用数组等能找到前驱的数据结构来实现:
- 判断全串是否回文 ==> 可用头尾(对向)双指针向中点遍历;
- 获取最长回文子串内容:5.最长回文子串
- 遍历字符串,获取以
[i, i]、[i, i+1]为回文中点的子串; - 判断子串是否回文:传入回文中点
l和r,向两侧(背向双指针)扩散(遍历判断),l == r时回文子串长度为奇数。
- 遍历字符串,获取以
根据字符数组构造回文串;- 最长回文子序列:动态规划
- 子串:是字符串中连续的一个序列;
- 子序列:是字符串中保持相对位置(删除某些字符)的字符序列;
- 如,
"bbbb"是字符串"bbbgb"的子序列但不是子串。
1 | |
方法二、用链表来实现:
- 链表快慢指针技巧
-
判断全串是否回文:234.判断回文链表 对称链表,经典例题。
- 数组快慢双指针找前半部分链表的尾节点(链表中点,奇数找中点前一个节点,偶数找前一个中点);
- 封装函数:(头插法)反转后半部分链表;
- 遍历短链表(即第二个),比较同向双指针,空间复杂度
O(1)。 - 反转还原后半部分链表并返回结果。
滑动窗口
左右指针技巧中,把索引左闭右开的区间 [left, right) 称为一个「窗口」,长度为 right - left。方便边界处理, [0, 0)中没有元素,[0, 1)中有一个元素 0。
滑动窗口:保证每个窗口里字母都是唯一的。双指针的一种,大多与不重复字符有关。
核心思想:维护一个左闭右开的窗口,不断滑动,左右指针交替前进( 不回头 ),更新答案。
- 虽然有嵌套的 while 循环,但时间复杂度依然是
O(n),因为每个元素都只会进入和被移出窗口一次。
滑动窗口4类经典例题:
-
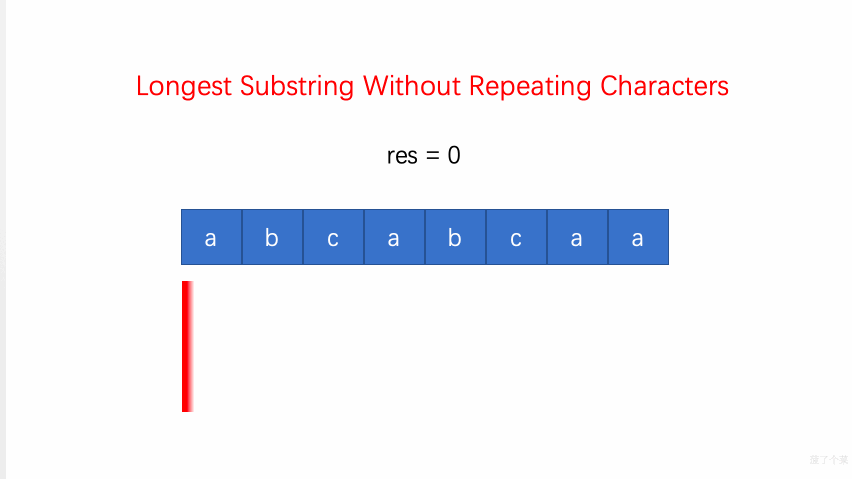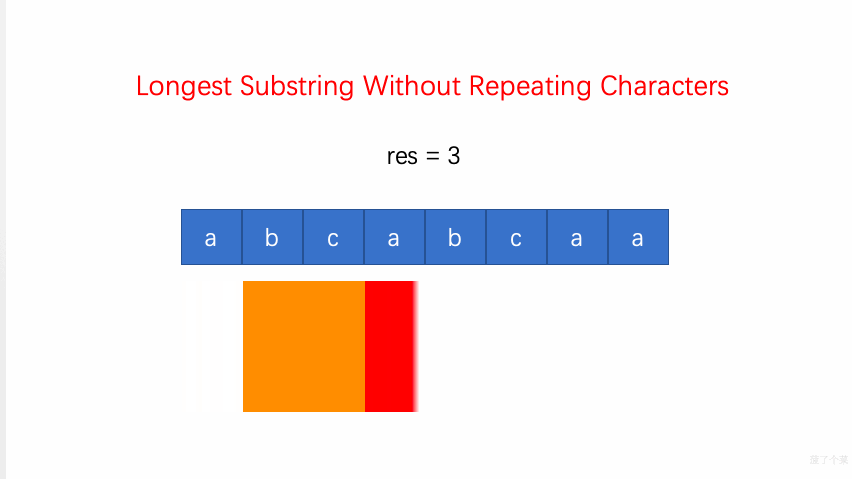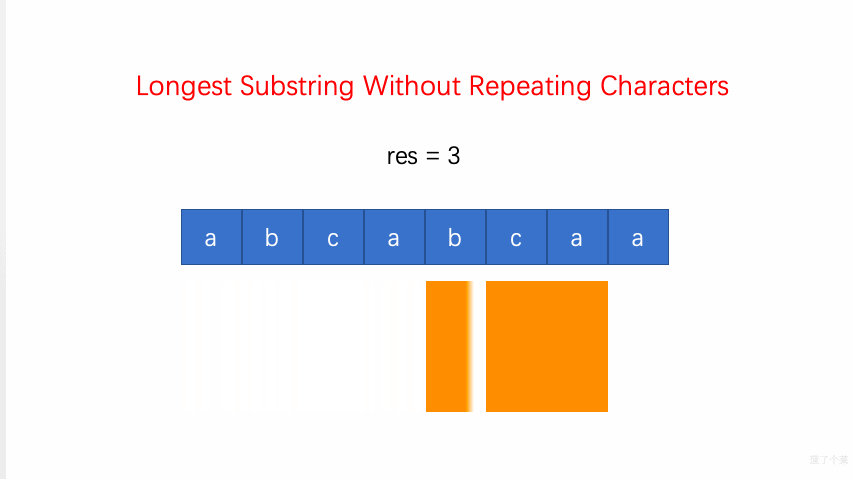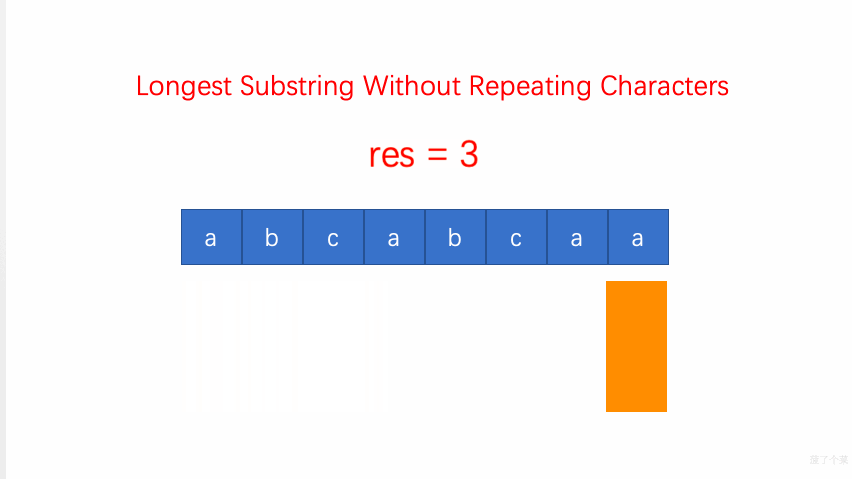
3.无重复字符的最长子串:当 window 内出现重复字符(HashMap 中已有当前字符)时,则调整左边界
left = Math.max(window.get(ch) + 1, left)(val 为字符对应的窗口结束位置,+1表示被重复字符的右侧);调整(右移并更新)right边界,更新子串及其长度;O(N)-
剑指 Offer 48.最长不含重复字符的子字符串:也可用动态规划,但为
N^2。如subDp[i]表示[0, i]区间内最长不含重复字符的子串,subDp[i] = Math.max(subDp[i-1], longestSub),从 i 不断向前遍历可得到longestSub=(j, i],表示以 i 索引位置结尾的不含重复字符的最长子串。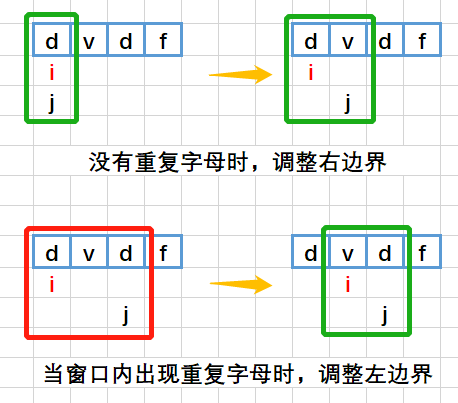
-
-
最小窗口:76.最小覆盖子串:包含
Target所有字符的、当前字符串Source的最短子串;-
步骤:十分经典的
HashMap代码need和window相当于计数器,分别记录 T 中(需凑齐的)字符数量和窗口中对应字符的出现次数;-
寻找可行解:先不断增加
right指针扩大窗口[left, right),直到窗口中的字符串符合要求(包含了T中所有字符);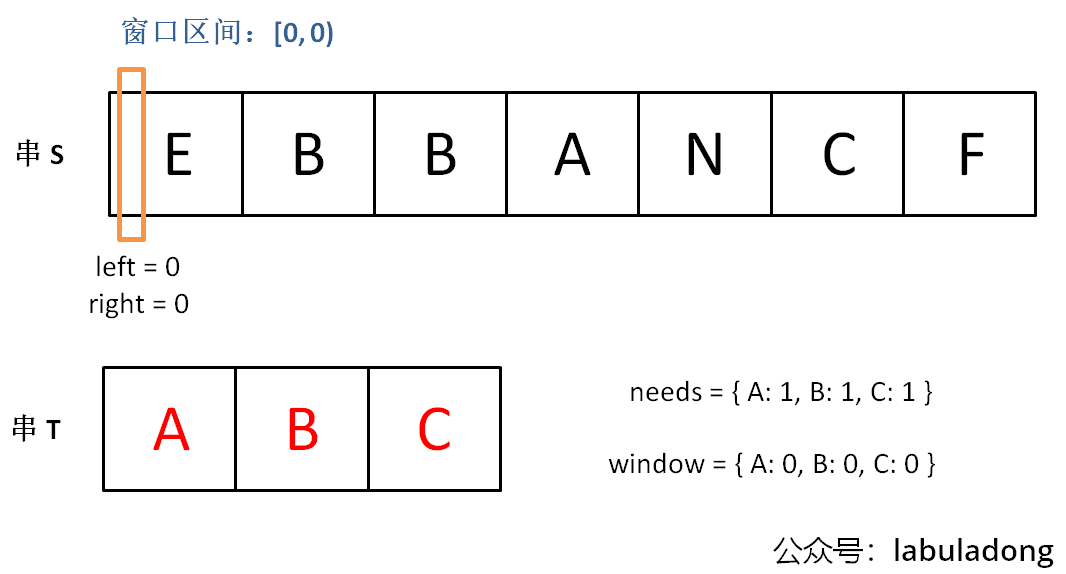
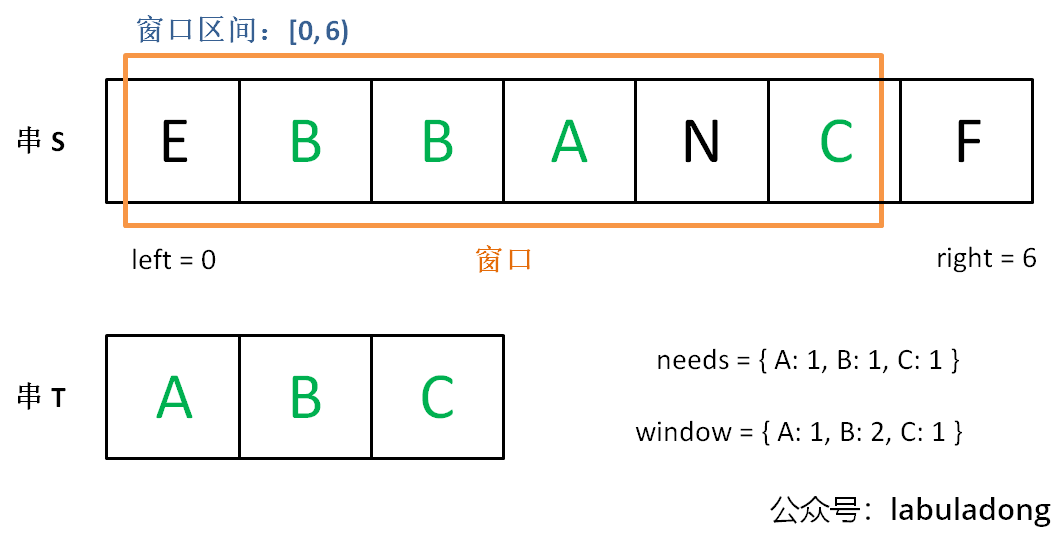
- 优化可行解:再不断右移
left指针缩小窗口,更新窗口的起始索引及长度,直到窗口不再符合要求(不包含T中所有字符)。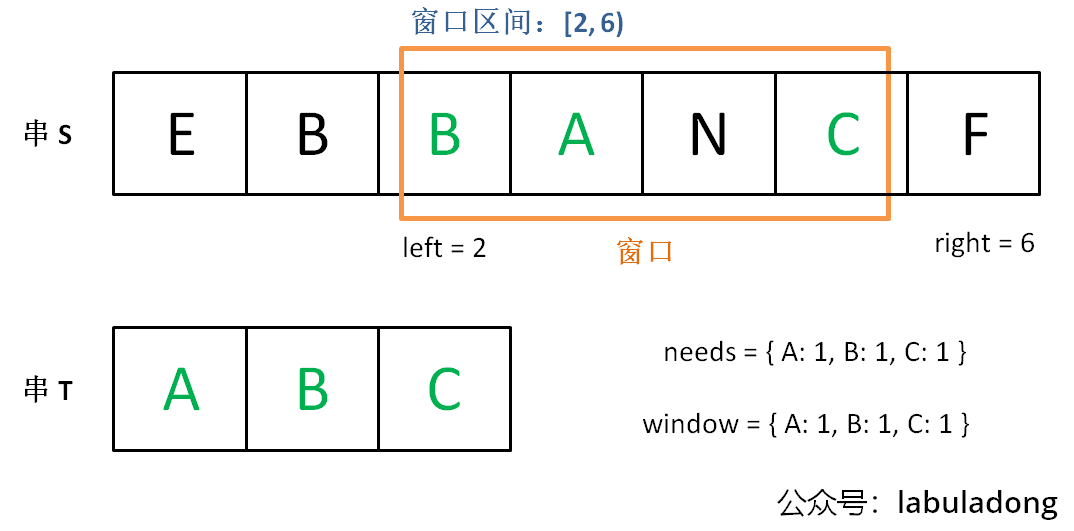
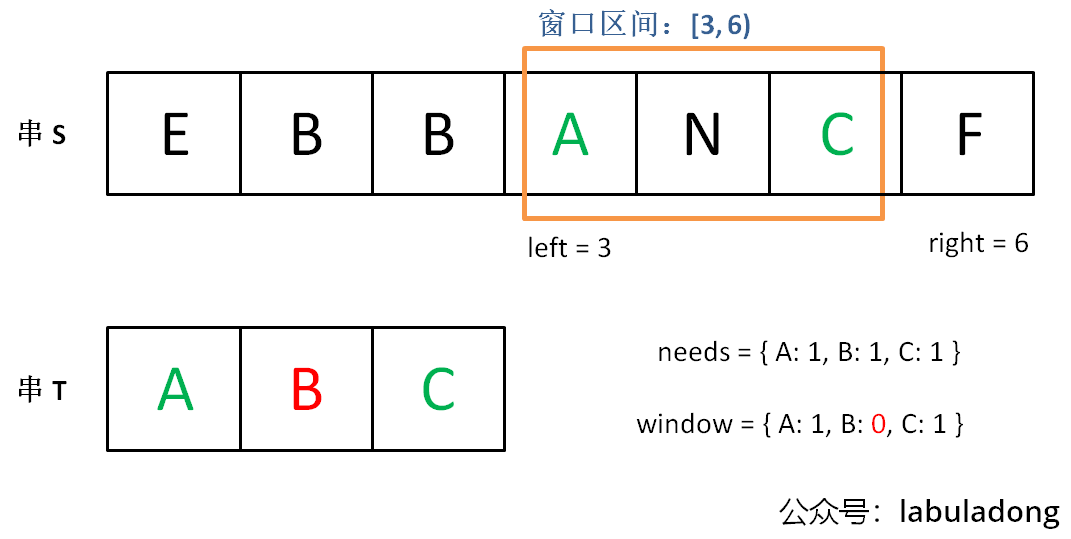
-


滑动窗口框架:
1 | |
经典例题
-
String 类的常用方法:见 String 类;
-
统计字符串中每个字符出现的频率:
-
出现次数最多字符
- 剑指 Offer 50.第一个未重复的字符
- 字符串运算:将所有重复的字符替换为
""; 哈希表;
- 字符串运算:将所有重复的字符替换为
-
剑指 Offer 05.替换空格:常规方法为遍历
charAt(i);1
2
3
4
5
6
7
8StringBuffer res = new StringBuffer(); return res.toString(); // 将char转为String,并比较 String.valueOf(ch).equals(” “) str.replaceAll(”\s“, ”%20“); // 模式匹配 str.replace(” “, ”%20“); -
简化复杂 url
-
14.字符串数组的最长公共前缀:先用
Arrays.sort(strs)为字符串数组升序排序,再从前往后遍历、对比第一个和最后一个字符串的字符。 -
-
1
2
3
4
5
6StringBuffer ans = new StringBuffer(); while (i >= 0 || j >= 0 || add != 0) { int x = (i >= 0) ? num1.charAt(i) - ’0‘ : 0; } // 答案需翻转 ans.reverse();
-
- 剑指 Offer 58-I.翻转单词顺序
- 常规方式:将字符串
s按空格split成若干单词,然后reverse,把单词join成句子。用了额外的空间。 - 原地翻转:将字符串
s反转,然后将每个单词分别反转再join(); - 用正则匹配分割单词,放入String数组,反转数组再
join()。
- 常规方式:将字符串
-
剑指 Offer 58-II.左旋转字符串:字符串前 n 位原地移动到尾部;
- 切片函数 + 拼接;
StringBuilder(),用 i 遍历[n, len + n],取余i % len。
KMP 字符串模式匹配算法
“暴力搜索”会反复回溯主串,导致效率低下,而 KMP 算法可利用已遍历部分匹配这个有效信息(部分匹配表),保持主串上的指针不回溯;通过修改子串的指针,让模式串尽量移动到有效的位置。
- 应用了贪心算法。用来解决字符串查找的问题,可在字符串(S)中查找子串(W)、模式串(P)出现的位置。
- 把字符匹配的时间复杂度缩小到
O(m + n),空间复杂度也只有O(m)。

根据部分匹配表(next 数组),最后一个匹配字符B(在已匹配的字符串中)对应的”部分匹配值”为2。移动位数 = 已匹配的字符数 - 对应的部分匹配值。
- 前缀:指除了最后一个字符外,字符串的全部连续字符组合;
- 后缀:指除了第一个字符外,字符串的全部连续字符组合。
- 部分匹配值:”前缀”和”后缀”的最长共有元素的长度。
- 如
"ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- 如
- “ABCDAB“中有两个
"AB",”部分匹配值”就是 2(”AB”的长度)。搜索词移动时,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可来到第二个”AB”的位置。 - 字符串匹配的KMP算法 阮一峰
链表
数组 VS 链表 、ArrayList VS LinkedList。链表相关的题目套路比较固定,主要是双指针技巧。
头指针 VS 虚拟头结点
指针:Java 语言中不存在指针,但可理解为引用。
-
指针丢失:指针没有明确指向。
-
内存泄漏:结点不判空就操作
next域等,导致空指针异常。
头结点:在单链表的第一个结点前附加一个结点,称为头结点。头结点的 Data 域可为空,仅包含 next 域;也可记录表长等信息。
头指针:指向链表的第一个节点,通常用来标识一个链表,如单链表 L。
- 若不带头结点:
- 头指针指向第一个节点的存储位置;
- 判空:头指针为
null(Java 区分大小写,且所有关键字都是小写)时表示一个空链表。
- 若带头结点:
- 头指针指向头结点的存储位置;
- 判空:头结点的
next域为null时为空链表。
优点:统一头/非头节点、空/非空链表的操作。
- 第1个节点位置的插入、删除与其他位置的操作保持一致。
1 | |
判断边界 / 特殊情况:
- 链表为空时,判空;
- 链表只包含一个、两个结点时;
- 在处理头结点和尾结点时。
链表快慢双指针
单链表大部分都适用数组快慢双指针技巧。
1 | |
- 剑指 Offer 22.查找倒数第k个节点:即正数第
n - k + 1个结点,但n无法直接得到(计算链表的 length、栈),可用快慢双指针;注意k > n时应返回null。- 虚拟头结点技巧:为了防止空指针,如链表共有 5 个节点,删除倒数第 5 个(即正数第一个)节点,需先找到倒数第 6 个节点,但第一个节点前已没有节点。
-
876.链表的中间结点:慢指针走一步,快指针走两步。
while (fast != null && fast.next != null)。偶数返回第一个节点。- 143.重排链表:找链表中点,合并原链表的左半端和反转后的右半端【】;改变链表内部值。
- 19.删除倒数第 K 个结点 :调用查找函数,获取倒数第
k + 1个结点的引用,删除后继结点;
- 19.删除倒数第 K 个结点 :调用查找函数,获取倒数第
- 143.重排链表:找链表中点,合并原链表的左半端和反转后的右半端【】;改变链表内部值。

1
2// 删除倒数第 k 个,要先找倒数第 k + 1 个节点 ListNode pre = findKthFromEnd(dummy, k + 1); -
判断回文链表:见字符串中的回文串;
- 141.检测链表中是否有环:
slow和fast指针相遇即有环;【】-
142.环形链表 II 找环起点: 遍历
fast直到链表尾部,fast为slow的两倍速迟早会追上,fast、slow相遇(位置一定在环内)即跳出循环;无环则fast、slow将相继到达链表尾部,相遇时均为null;有环则fast指针在环内,slow以head为起点重新开始,fast、slow第二次相遇即为环起点;环起点不一定在head;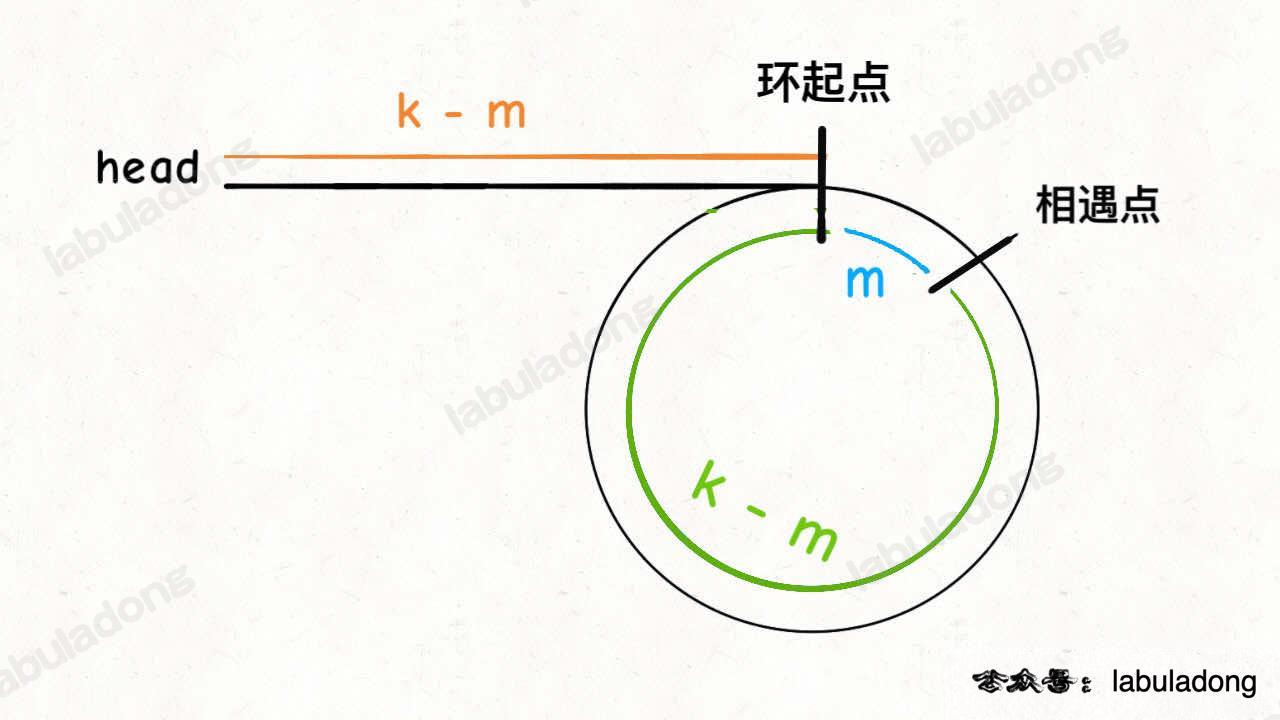
-
-
160.相交链表:判断两单链表是否相交;【】
-
剑指 Offer 52.两链表的第一个公共节点:找出交点(第一个公共结点);
- 方法一:用
HashSet记录一个链表的所有节点,和另一条链表对比,缺点是需额外空间; - 方法二:在逻辑上拼接两条链表,让
pa遍历完链表A后开始遍历链表B,if (pa == null) { pa = headB;},pb遍历完链表B后开始遍历链表A,此时二者长度相等,且pa和pb能同时到达相交节点c。空间复杂度O(1)。 - 方法三:两条链表首尾相连,问题转换成了「寻找环起点」。
- 方法四(常规思路):预先计算两条链表的长度,较长的链表
fast指针先走,使p1和p2到达尾部的距离相同,p1 == p2且不为空时即相交。
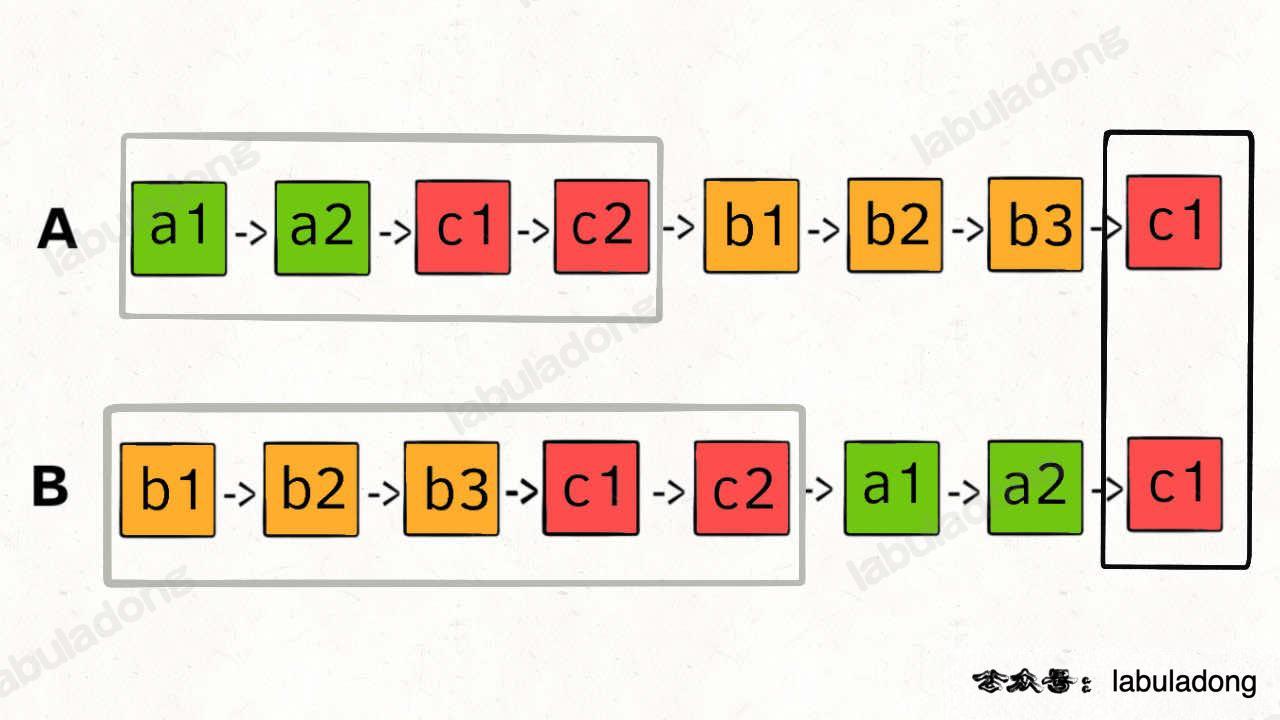
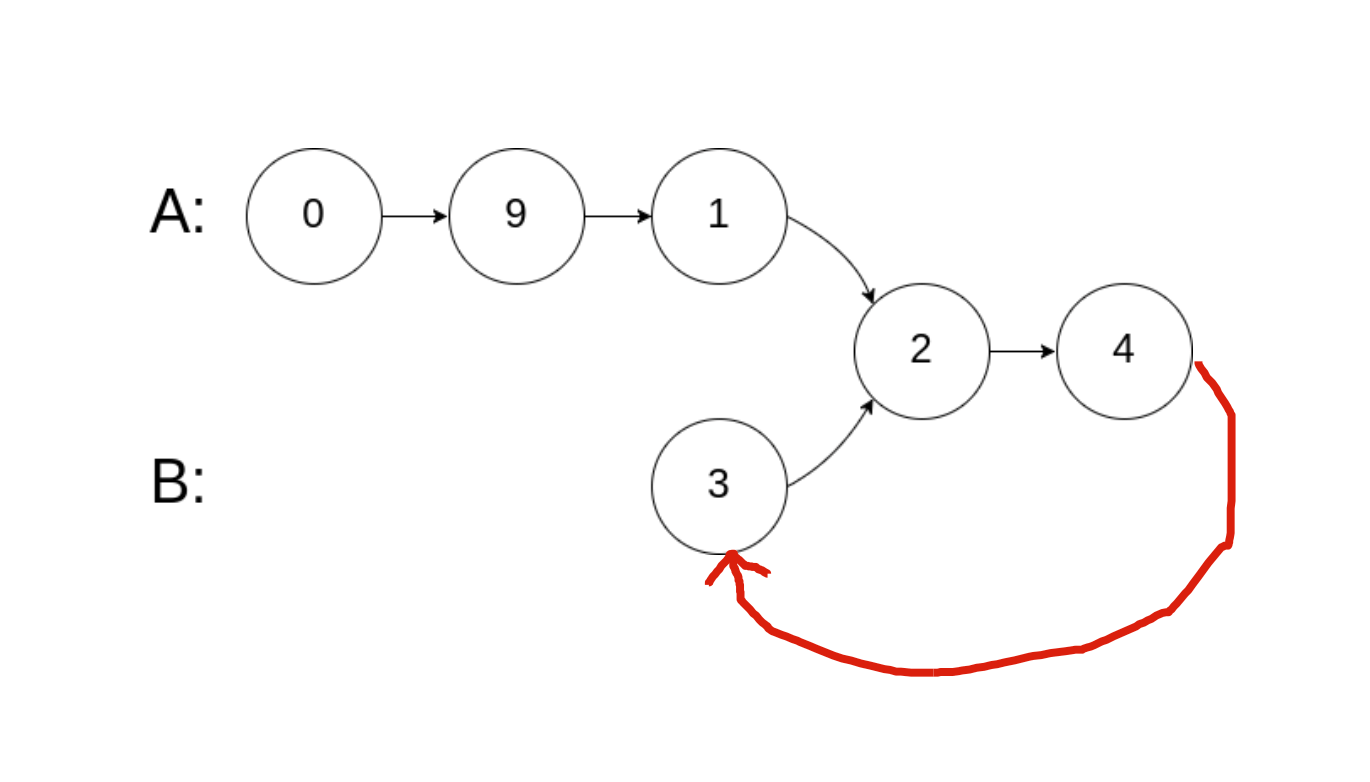
- 方法一:用
-
- 循环左移
链表双指针
-
剑指 Offer 25.合并两个排序的链表:拉链法 / 归并法 (2-路)归并排序
- 23.合并K个升序链表:第K个元素
1
2
3
4// 虚拟头结点 ListNode dummy = new ListNode(-1); // 合并后l1、l2最多只有一个非空,直接将链表末尾指向未合并完的链表 p.next = (l1 == null) ? l2 : l1; -
链表整数位运算
-
2.逆序链表按位表示整数 两数逐位相加 链表求和:carry 表示进位;
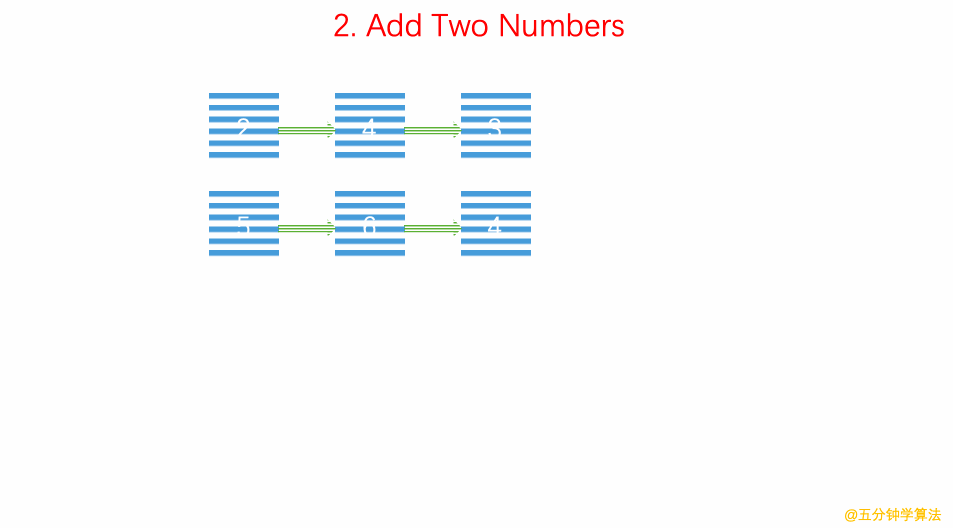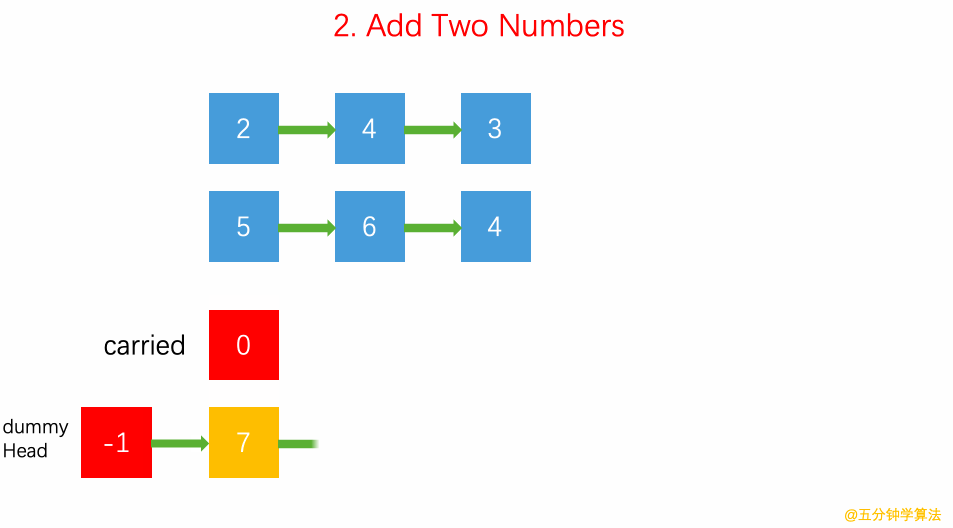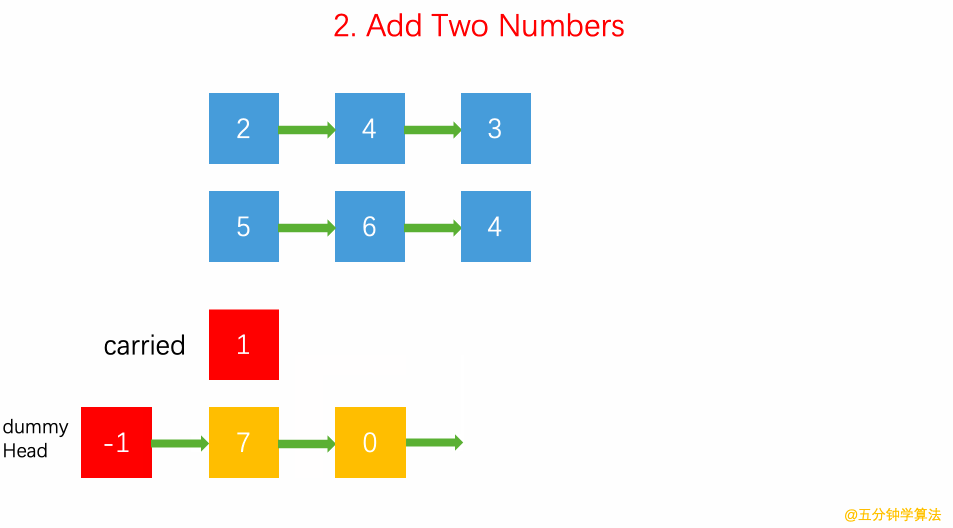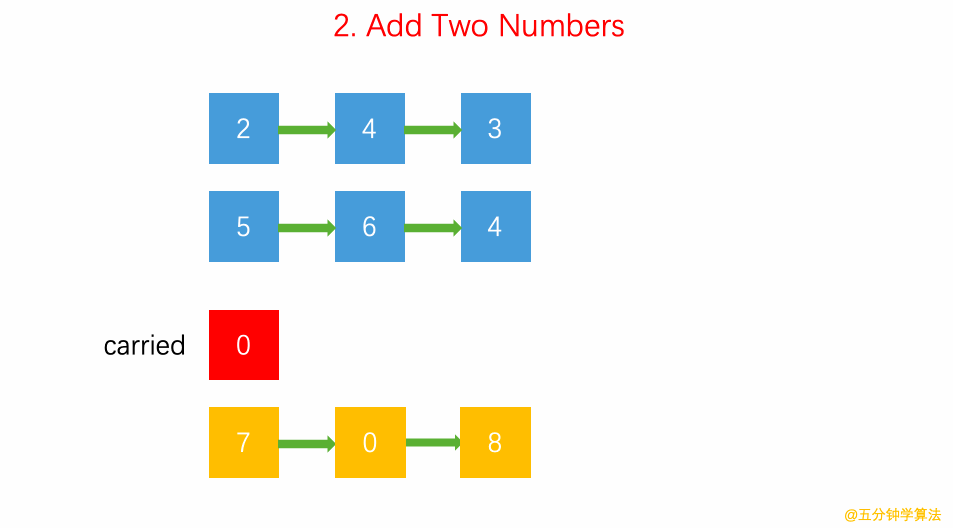
-
-
328.拆分链表的奇偶节点:
odd、even奇偶双指针交替前进;even.next不能为空;odd.next = evenhead;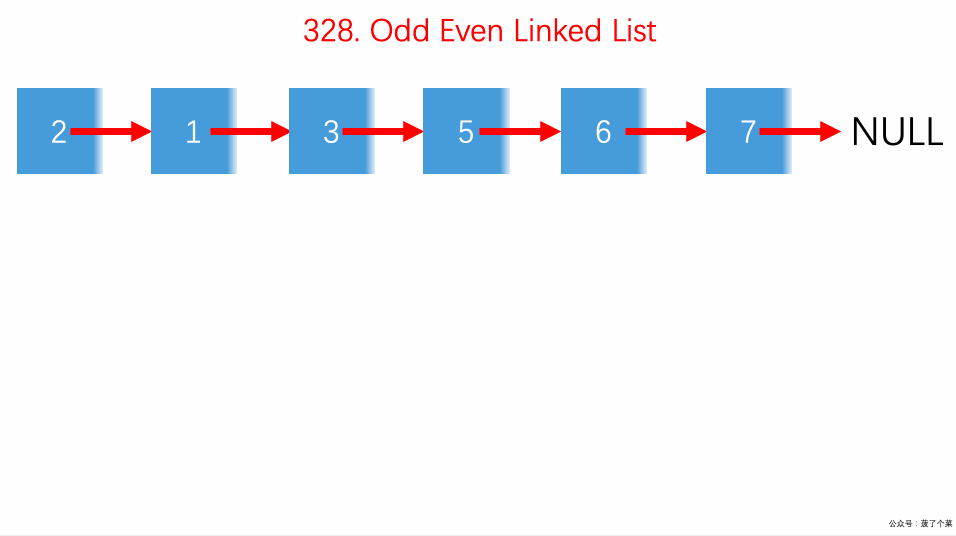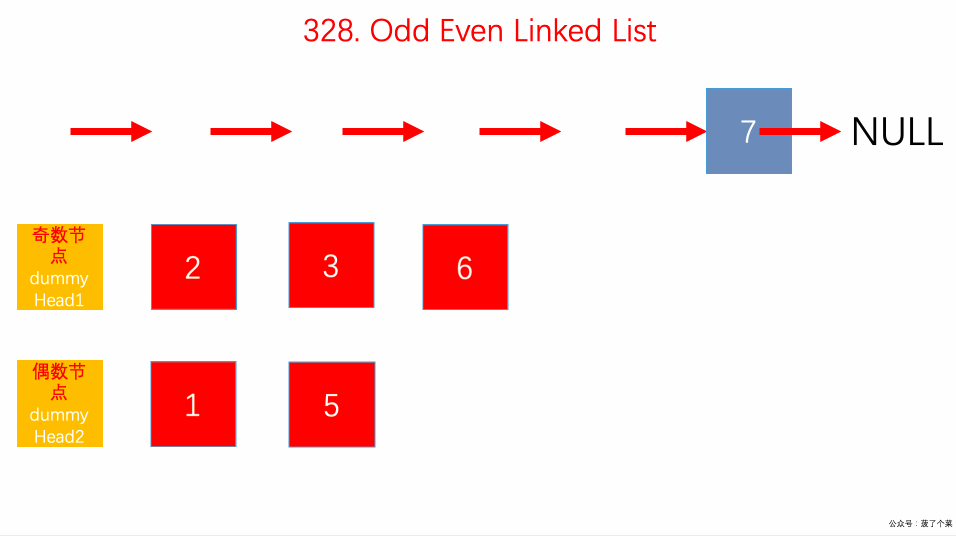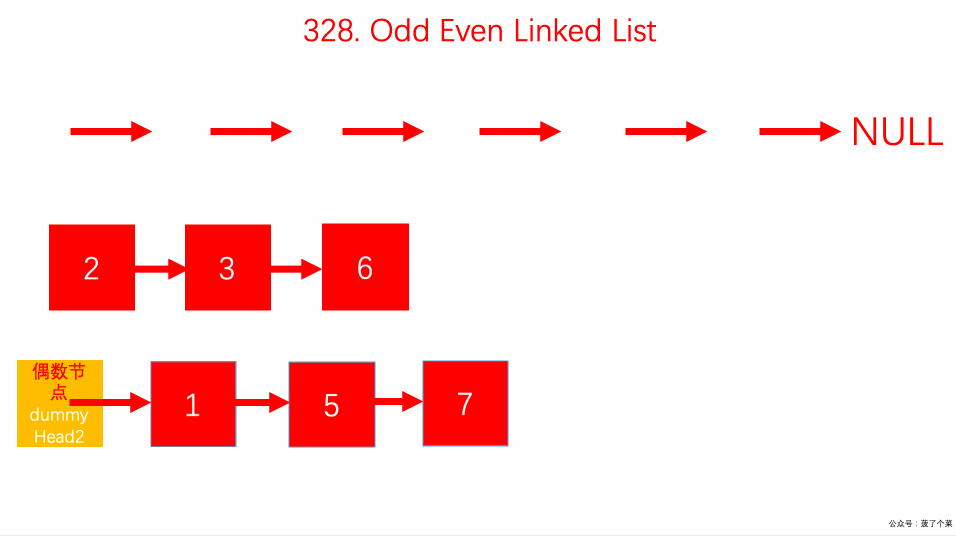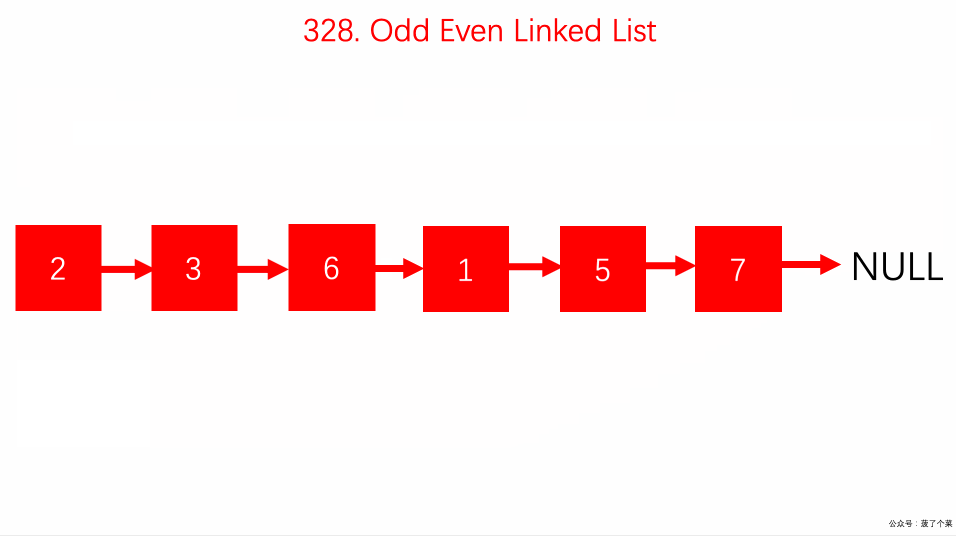

- 148.链表插入排序:【】
- 42.接雨水总数:【】
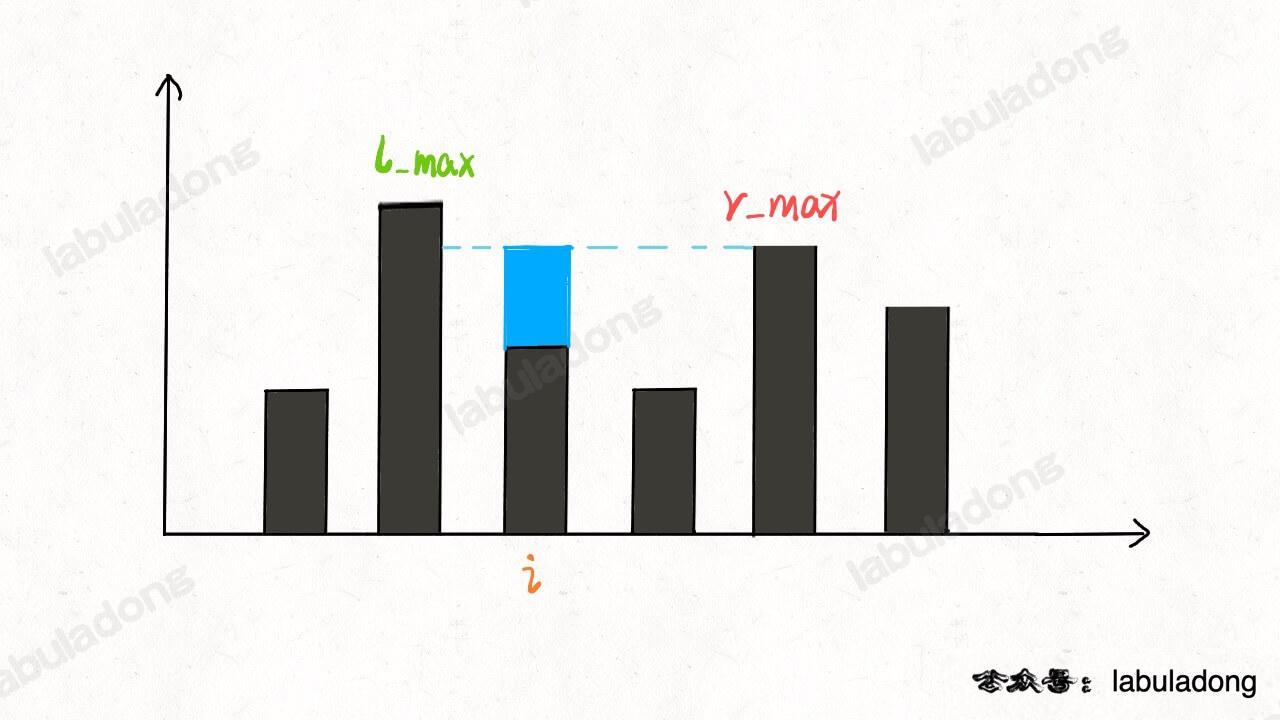
1 | |
经典例题
-
- 头插法:不申请额外空间,就地反转,空间复杂度
O(1); - 反转 => 栈:剑指 Offer 06. 从尾到头打印链表;
-
递归:
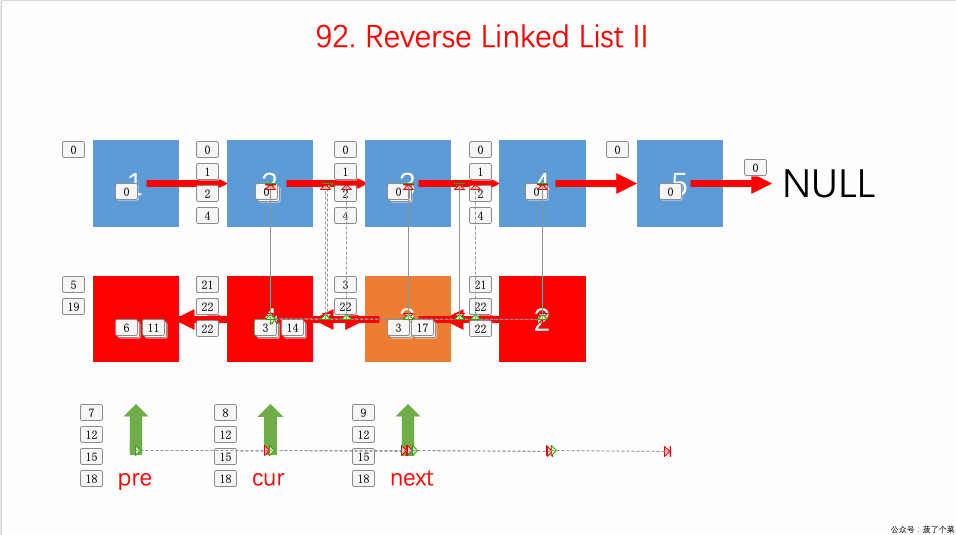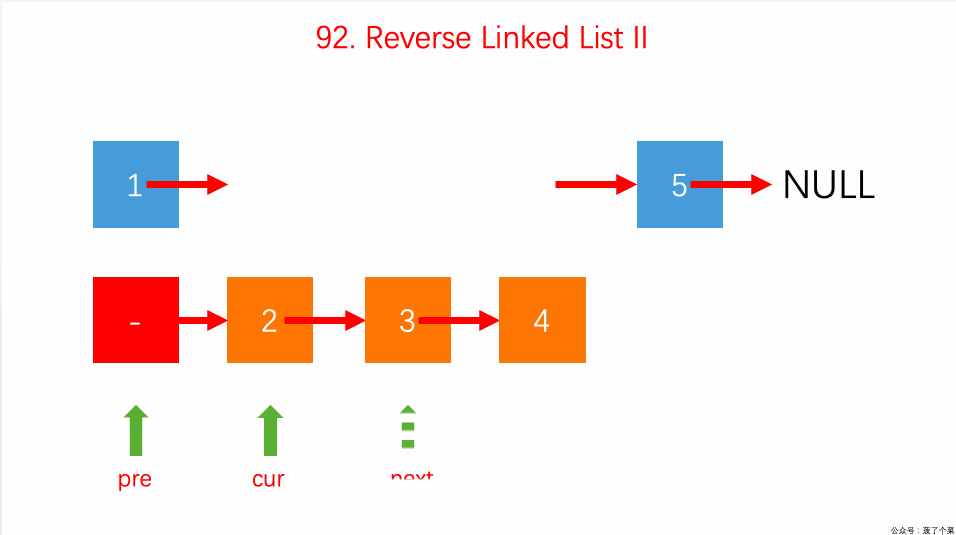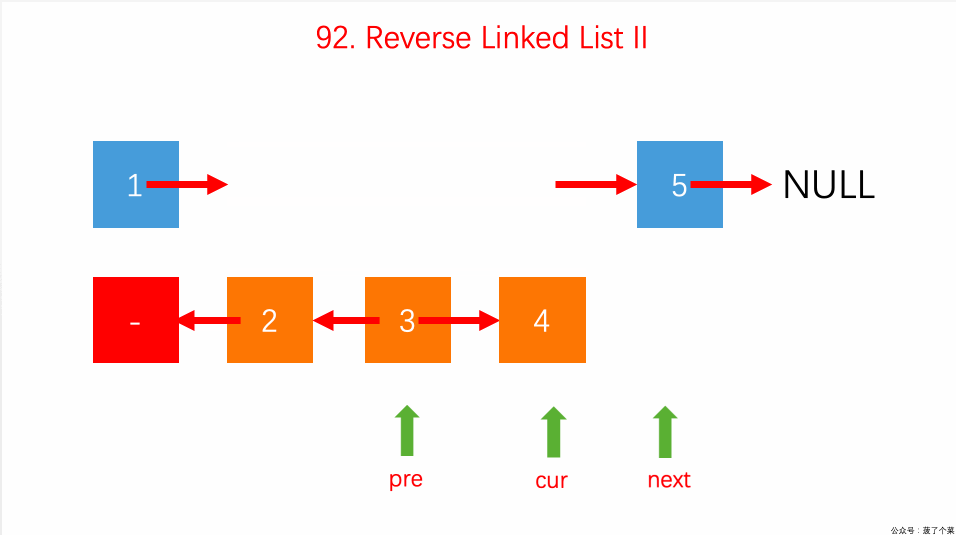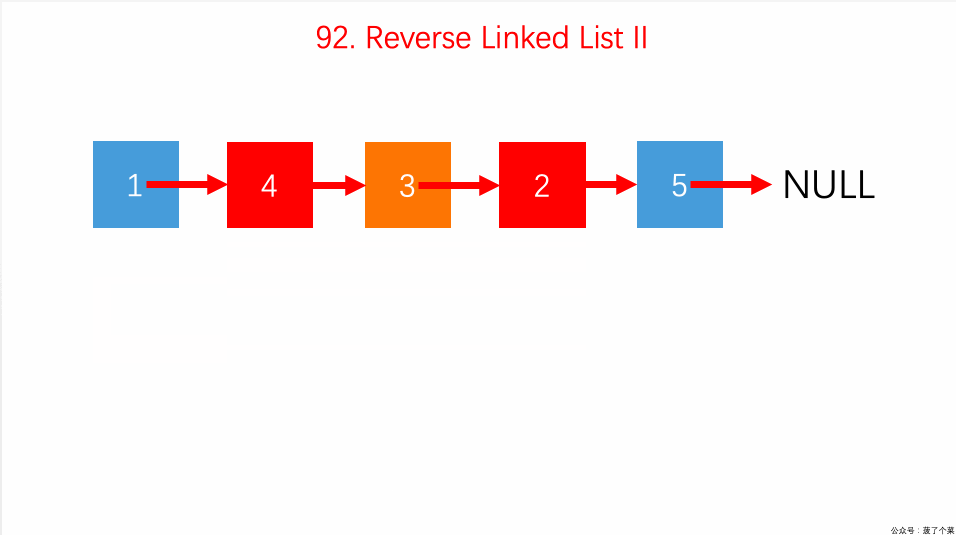
- 92.反转链表 II 指定区间:【】
- 迭代解法很简单,用一个 for 循环反转链表区间即可;
- 常用来考察纯递归的形式。
-
25.K 个一组翻转链表:
reverseKNode原地反转[head, tail)区间的元素,递归反转后续链表并连接起来。- 24.两两交换链表中的节点:相当于
K = 2的特殊情况,可用简化的多指针;【】

- 24.两两交换链表中的节点:相当于
- 92.反转链表 II 指定区间:【】
- 头插法:不申请额外空间,就地反转,空间复杂度
-
剑指 Offer 35.复杂链表的深拷贝 random 指针:
- HashMap + 递归;
- 第一次遍历复制并后插,第二次复制随机指针并分离链表【】;

-
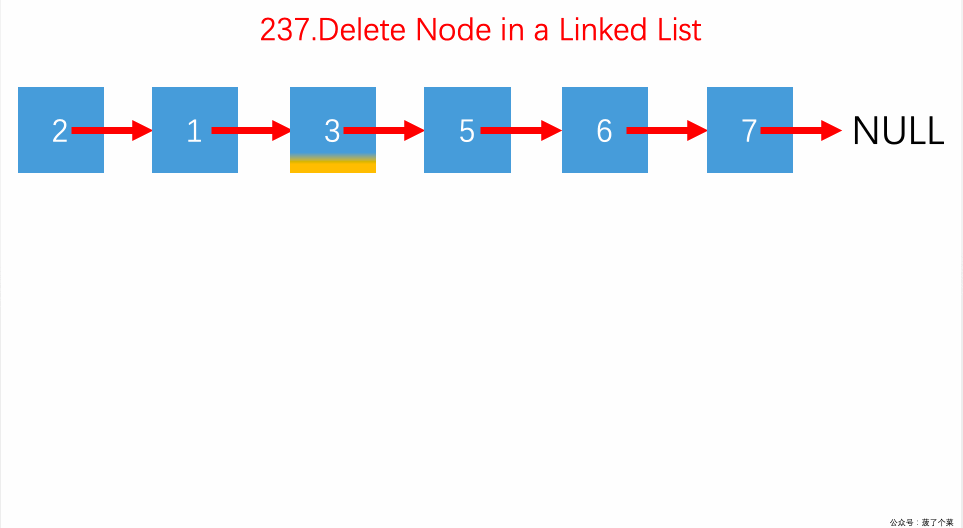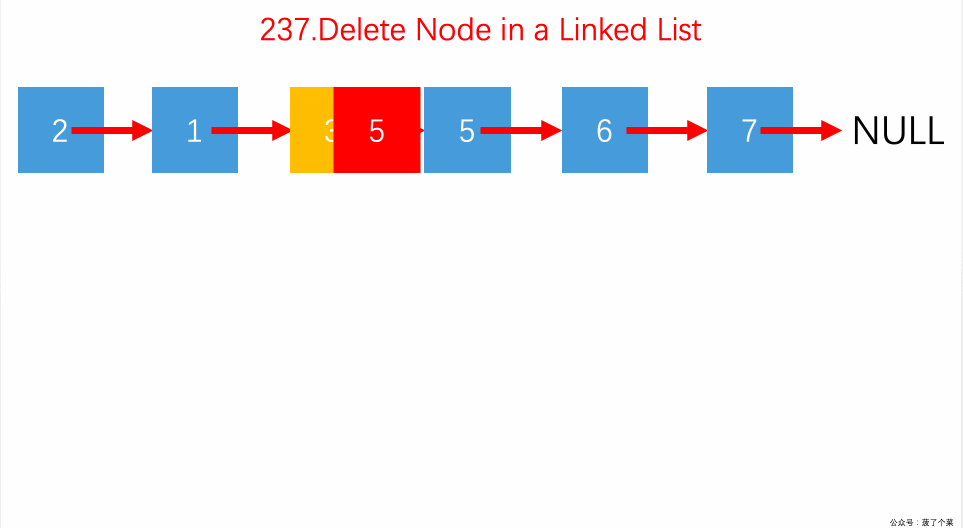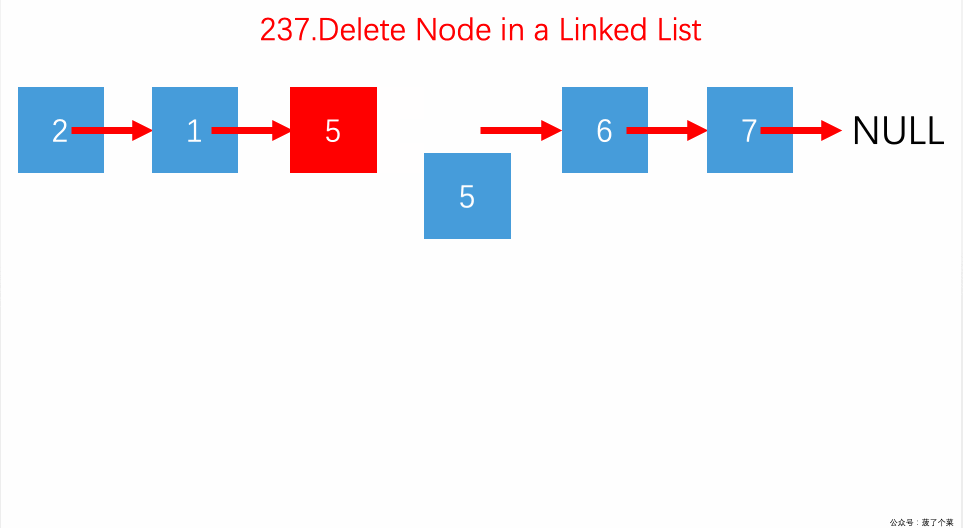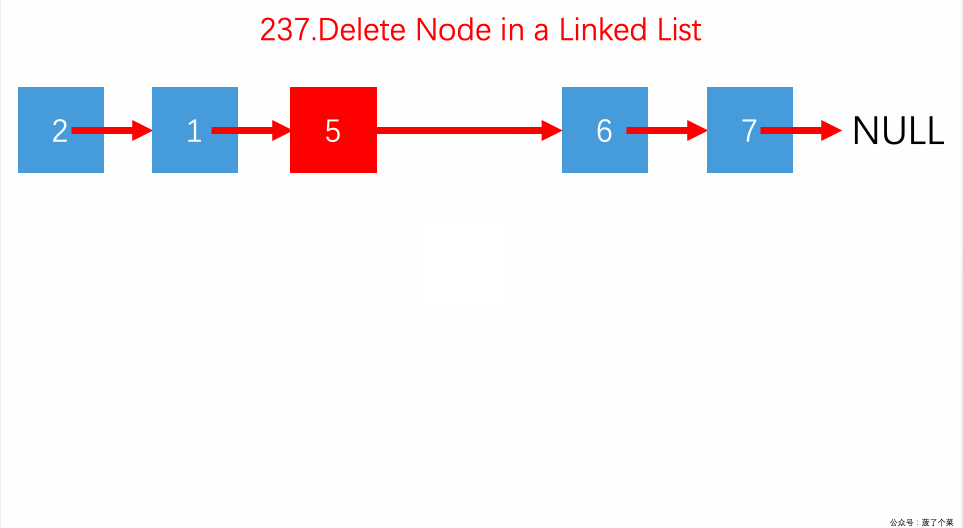
237.删除链表中的特定节点:不给头结点,只给要被删除的节点;前后节点交换值,删后继。【】
奇数位升序,偶数位降序,要求输出全局升序,不用数组- 双向链表
- 前插:右下(指向后继)+ 顺时针
- 后插:左下 + 逆时针
- 删前驱:
- 循环链表
- 双向循环链表
1 | |
跳表
跳表(Skip List):基于链表实现的有序列表,使得包含n个元素的有序序列的查找和插入操作的平均时间复杂度都是 O(logn),优于数组的 O(n)复杂度。对并发友好。
实现:快速的查询效果是通过维护一个多层次的链表(ConcurrentSkipListMap)实现的,实现了快速查询效果将平均时间复杂度降到了O(logn)。这是一个典型的用空间换时间数据结构。
缺点:就是“以空间换时间”方式存在一定数据冗余。
应用:Redis中的有序集合对象的底层数据结构就使用了跳表。
栈、队列
栈
栈常用一维数组或链表来实现:
- 用数组实现的栈叫作 顺序栈,
- 用链表实现的栈叫作 链式栈 。
1 | |
队列
队头(front)出队,队尾(rear)入队;

-
顺序队列(数组实现):存在“假溢出”的问题(即明明有位置却不能添加)。因为在数组中
front和rear会持续向后移动,无法返回数组起始位置,数组长度固定,导致数组越界、前端有大段空白。- 队列空:
front == rear; - 队列满:
rear - front == QueueSize; -
循环队列:可解决假溢出和越界问题。
- 队列空:
front == rear,排除队列溢出的情况; -
队列满:
(rear + 1) % QueueSize == front,即rear在front前一个位置 。
- 队列空:
- 队列空:
-
链式队列(链表实现)
常用于:
- 阻塞队列;
- 线程池中的请求/任务队列;
- Linux 内核进程队列;
- 消息队列;
Deque 双端队列
集合框架,用于实现栈和队列。
PriorityQueue 优先队列
出队顺序按照优先级的队列;常用于找最值,往往用二叉堆来实现。用于有动态添加、删除数据且需获得最值的场景。手撕算法典型题包括:
要理解以下关键点:
- 优先级队列是一种能自动排序的数据结构,增删元素的复杂度是
O*(log*N),底层使用二叉堆实现。 - 二叉堆是一种拥有特殊性质的完全二叉树。
- 优先级队列(二叉堆)的核心方法是
swim, sink,用来维护二叉堆的性质。
至少需支持下述操作:
- 插入带优先级的元素(offer/insert_with_priority);
- 查看或取出最高优先级的元素(peek、
poll/pull_highest_priority_element);
其它可选的操作:
- 清空优先队列;
- 调整一个元素的优先级;
- 批量插入元素;
- 检查优先级高的一批元素;
- 合并多个优先队列;
单调栈、单调队列
单调栈:每次新元素入栈后,栈内的元素都保持有序。用途不广,只处理一类典型的问题。
- 用于:快速计算下一个更大/更小元素、上一个更大/更小元素。
单调队列:普通队列 + api,用于快速计算整个队列的最大/最小值。
- 496.下一个更大元素 I :由后往前对比数组元素和栈顶,逐个弹出,插入目标元素后再逐个入栈【】
经典例题
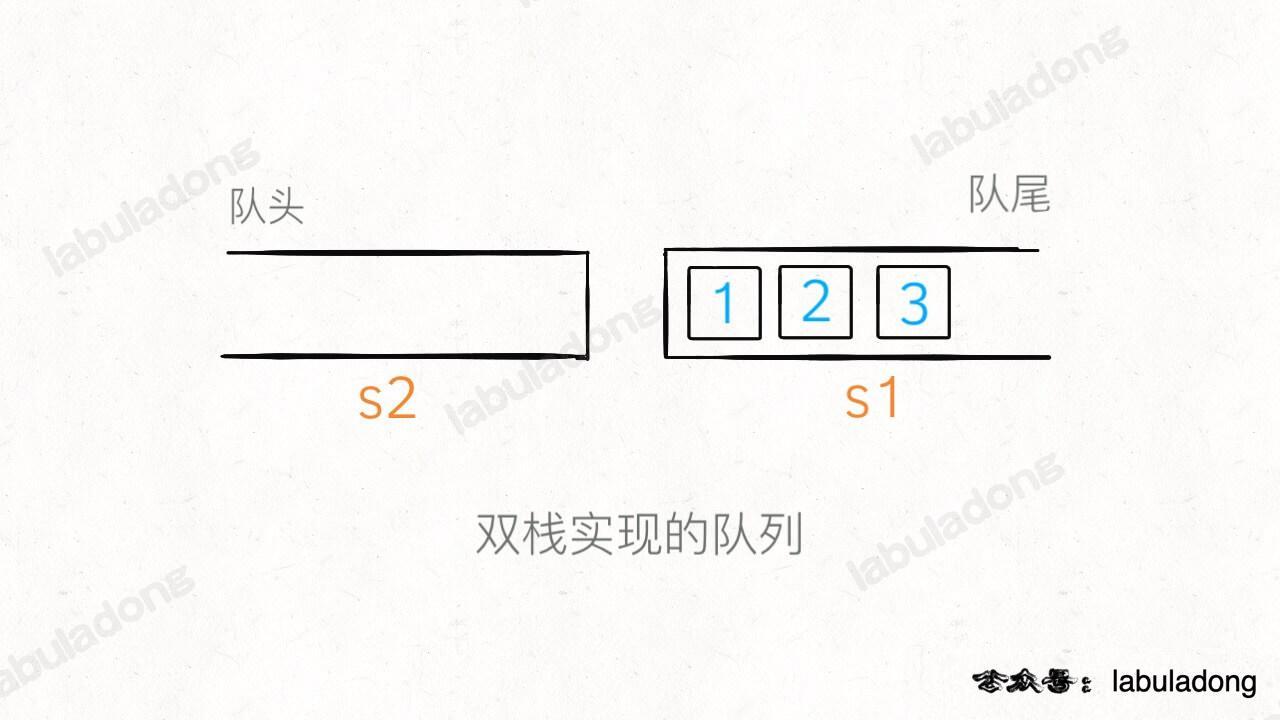
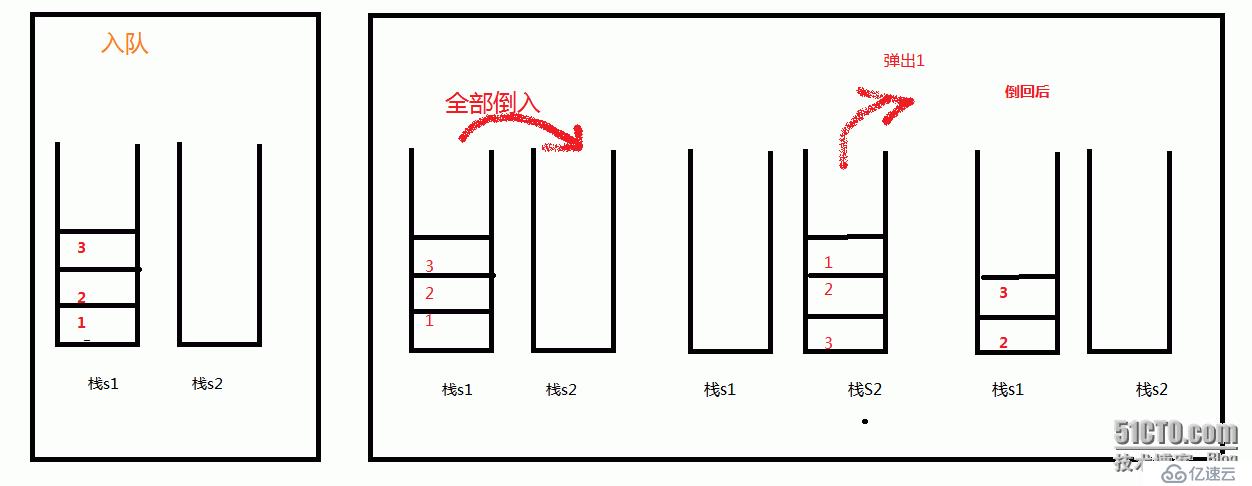
- 232.用栈实现队列:如用两个栈实现浏览器的回退和前进功能。
queue()构造:new 新栈stackIn(s1)和stackOut(s2);- 队尾(rear)入队(
push/offer/add):stackIn.push(x)入栈; - 查看队头(peek):如果
stackOut为空,则stackIn全部倒入stackOut;栈顶top()即为队头; - 队头(front)出队(
pop/poll/remove):先调用peek()保证stackOut非空,stackOut出栈;出队结束,stackIn为空也不必重新倒回; isEmpty()判空:stackIn和stackOut均为空。
- 225.用队列实现栈:只需一个队列;
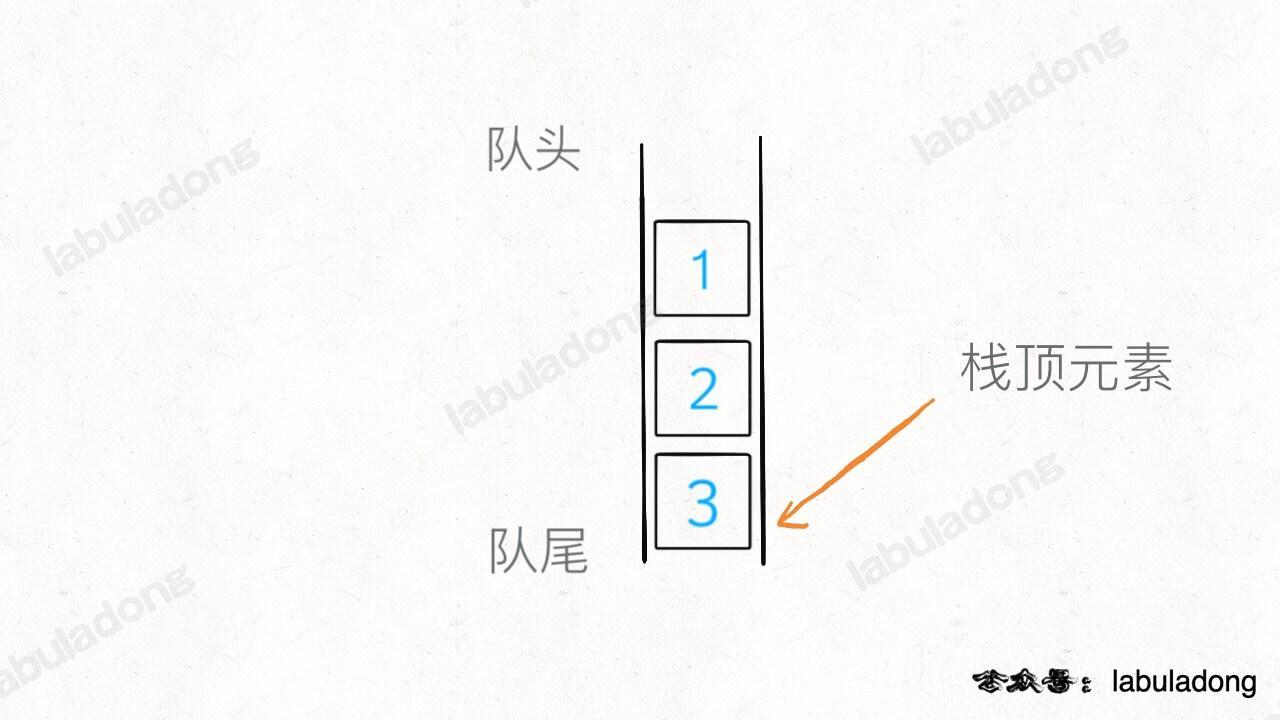
stack()构造:sz = 0,重新塞入时用于计数;push(x)入栈:queue.offer(x)入队;或维护topElem = x栈顶元素,x 是队列的队尾,是栈的栈顶topElem;pop()弹出栈顶:把队尾元素移到队头(把队尾前的所有元素出队再重新塞到队尾,顶过去),原队尾(现队头)poll()出队;或返回topElem,更新topElem为新队尾元素;top()查看栈顶:调用pop()弹出队尾元素(栈顶元素)后恢复(把队尾元素再次塞入队尾),sz++;isEmpty()判空:queue.isEmpty()。
-
20.判断有效的成对括号:
Stack保存所需的右括号 + HashMap 存左右括号对应关系方便查表,若ch为左括号,则将对应右括号入栈,若为右括号,则与栈顶元素对比;- 921.使括号有效的最少添加、1541.平衡括号的最少插入次数【】:计算多出的
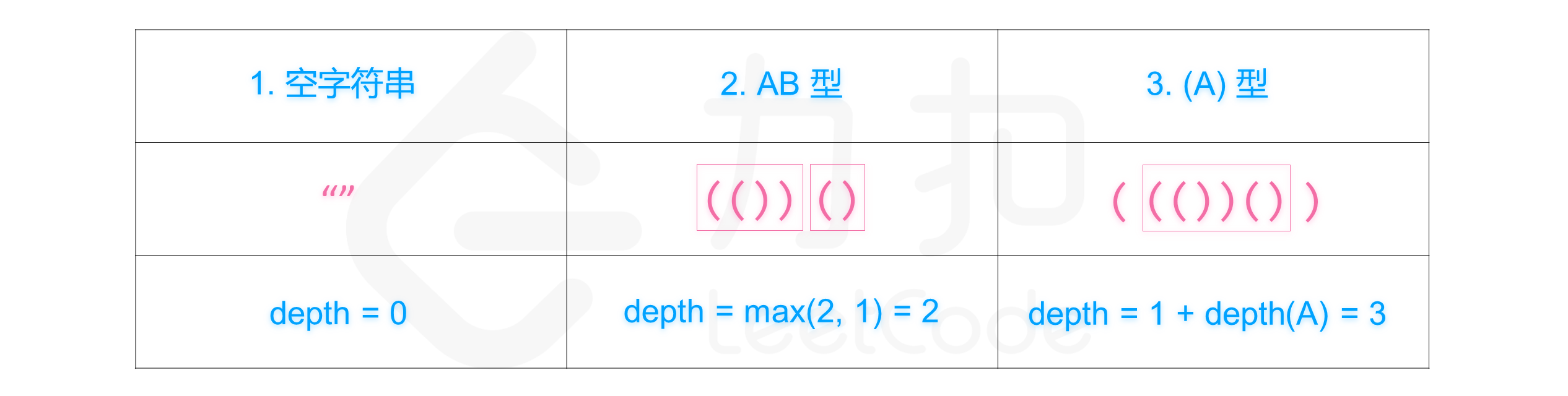
(或),need变量记录对右括号的需求数,(则need++,)则need--;当need == -1时,意味着遇到一个多余的右括号,显然需插入一个左括号。 - 1614.计算括号的最大嵌套深度:
depth++时,更新maxDep = Math.max(maxDep, depth); - 1111.根据嵌套深度 分成两个不相交的有效括号字符串:【】

- 921.使括号有效的最少添加、1541.平衡括号的最少插入次数【】:计算多出的
-
中缀表达式->后缀:根据中序结果构造二叉树,打印后序结果;
- 剑指 Offer 31.根据入栈序列、推断弹出序列:每次入栈后,弹出所有符合弹出序列顺序的栈顶元素;
- 150.逆波兰表达式求值:用栈计算后缀表达式;

- 316.去除重复字母:【】
bool[] inStack布尔数组保证栈中元素不重复;- 栈保证字符出现的顺序;
- 类似单调栈的思路,配合计数器
count不断 pop 掉不符合最小字典序的字符。
- 反转字符串:还可用背向双指针
哈希表
哈希表和常说的 Map(键值映射)是不是同一个东西?不是。
哈希表、散列表(Hash Table):用于存储键值对。
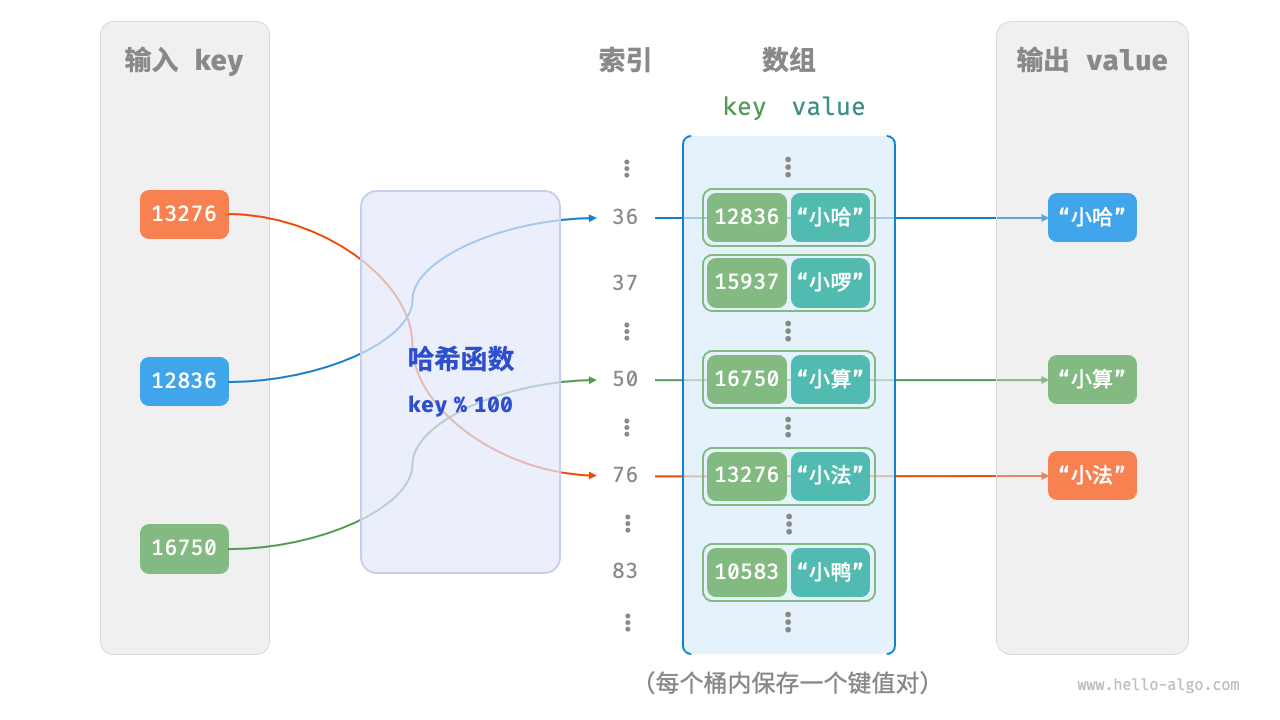
原理:哈希表的本质是数组 + 哈希函数。通过散列函数把键映射到一个数组(散列表)里,得到数组的索引,进而直接访问(快速存取)索引位置的值。+ 解决哈希冲突。
- 散列表:存放记录的数组。只不过数组存放的是单一的数据,而哈希表中存放的是键值对。
- 哈希函数(哈希算法、散列函数、映射函数):
- 作用是把任意长度的输入(键 key)转化成固定长度的输出(数组的索引)。
- 还要保证索引是合法的:输入相同的
key,输出也必须要相同,这样才能保证哈希表的正确性。
- 用于查找。
缺点:
- 哈希冲突;
- 最大缺点是:Hash 索引不支持顺序和范围查询。hash 表存储的是无序数据,范围查找时需遍历,遍历比较耗费时间。
- 将所有的数据文件添加到内存,比较耗费内存空间。
哈希冲突与扩容
哈希冲突、哈希碰撞:不同的 key 通过哈希函数可能得到相同的索引值。
哈希冲突是否可以避免?
-
哈希冲突不可能避免,只能在算法层面尽量处理。
-
哈希冲突是一定会出现的,因为这个
hash函数相当于是把一个无穷大的空间映射到了一个有限的索引空间,所以必然会有不同的key映射到同一个索引上。
解决方法:JDK1.8 前 HashMap 用链地址法解决,JDK1.8 后 HashMap 用红黑树(数组 + 二叉树);
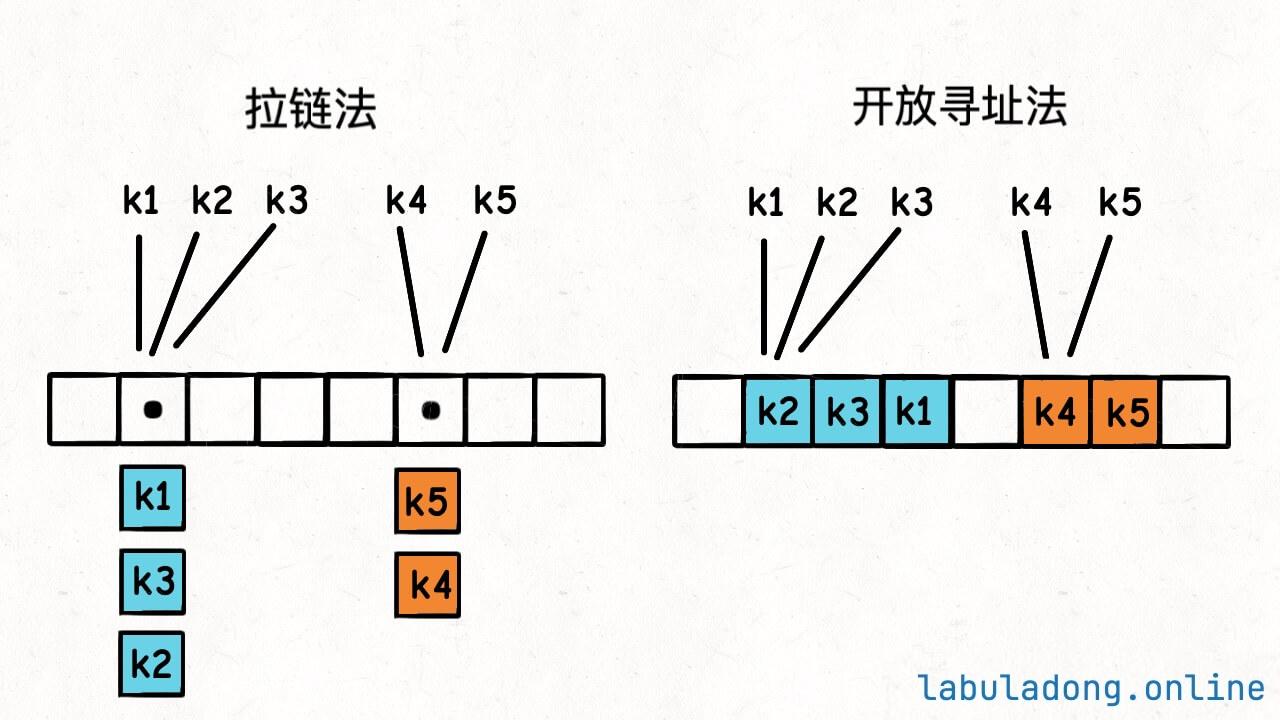
- 拉链法(纵向延伸思路):数组 + 链表,哈希表的底层数组并不直接存储
value类型,而是存储一个链表,当有多个不同的key映射到了同一个索引上,这些key -> value对儿就存储在这个链表中。需额外的空间存指针。 - 开放寻址法思想(横向延伸思路):数组特性,如果通过哈希函数计算出的索引所对应的空间已经被占用了,就再找一个还没被占用的空间将数据存进去。
- 线性探查法:继续向后一个位置找(连续寻址),直到找到空闲位置为止。
- 双重哈希法:继续用第二个哈希函数来计算索引,第二个被占用就用第三个,以此类推,直到计算出没被占用的空间对应的索引。
- 可以通过哈希表扩容来减少哈希冲突。
哈希表扩容
负载因子、装载因子(load factor):已插入元素的数量除以数组容量。用于衡量哈希冲突的严重程度,也常作为哈希表扩容的触发条件,装载因子超过某一阈值时就进行扩容。
- 例如在 Java 中,当负载因子超过 0.75 时,系统会将哈希表扩容至原先的 2 倍。
哈希表扩容时:缺点、过程
- 需将所有键值对从原哈希表迁移至新哈希表,非常耗时;
- 并且由于哈希表长度改变,需要(通过哈希函数来)重新计算所有键值对的存储位置,这进一步增加了扩容过程的计算开销。
为此,编程语言通常会预留足够大的哈希表容量,防止频繁扩容。
哈希表的性质
key 是唯一的,value 可以重复
哈希表中,不可能出现两个相同的 key,而 value 是可以重复的。
直接类比数组就行
为什么增删查改效率是 O(1)?
-
因为哈希表底层就是操作一个数组,其主要的时间复杂度来自于哈希函数计算索引和哈希冲突。
- 正常情况下,只要保证哈希函数的复杂度在 O(1),且合理解决哈希冲突的问题,那么增删查改的复杂度就都是 O(1)。
- 哈希表的增删查改效率不一定是 O(1) 。如果使用了错误的
key类型,比如用ArrayList作为key,那么哈希表的复杂度就会退化成 O(N)。
哈希表的遍历顺序可能会变化
哈希表中键的遍历顺序是无序的,不能依赖哈希表的遍历顺序来编写程序。
两个原因:
- 由于哈希函数对
key进行映射,所以key在底层table数组中的分布是随机的,不像数组/链表结构那样有个明确的元素顺序。 - 因为哈希表在达到负载因子时会扩容,会导致哈希表底层的数组容量变化,哈希函数计算出来的索引也会变化,所以哈希表的遍历顺序也会变化。
一定要用不可变类型作为哈希表的 key
所谓不可变类型,就是说这个对象一旦创建,它的值就不能再改变了。比如 Java 中的
String, Integer等类型。
- 因为哈希表的主要操作都依赖于哈希函数计算出来的索引,如果
key的哈希值会变化,会导致键值对意外丢失,产生严重的 bug。
加强哈希表
- 用链表加强哈希表:LinkedHashMap
- 用数组加强哈希表:ArrayHashMap
经典例题
-
- 哈希表法:
O(n); - 摩尔投票法:计数器,计数器为 0 时,假设 nums[i] 就是众数;遇到相同元素则
++,遇到不同元素则--,空间O(1)【】

- 哈希表法:
堆
定义
堆是一种树,任意一个节点的值都 >=(或 <=)其所有子节点的值。
- 最大堆
- 最小堆
用途:用于只关心最值:多次插入数据或 pop 最值后,再多次获取剩余元素的最(最大或最小)值(插入/删除 + 全体排序耗费资源太多)。
- 二叉堆的关键应用是Pri’orityQueue 优先级队列。如下面的23.合并K个升序链表。
优势
相对于有序数组,堆的主要优势在于更新(插入或删除)数据效率较高。
- 初始化:有序数组用排序算法;堆为
nlg(n); - 查找最值: 都是
O(1); - 更新(插入或删除)数据:
O(n),二分法为lg(n)+ 移动数据O(n);堆为lg(n)。
堆的存储
通常用完全二叉树的形式来表示、存储堆。也不一定全都是完全二叉树,如斐波那契堆和二项堆。
用数组存储二叉树既节省空间,又方便索引。
1 | |
插入元素
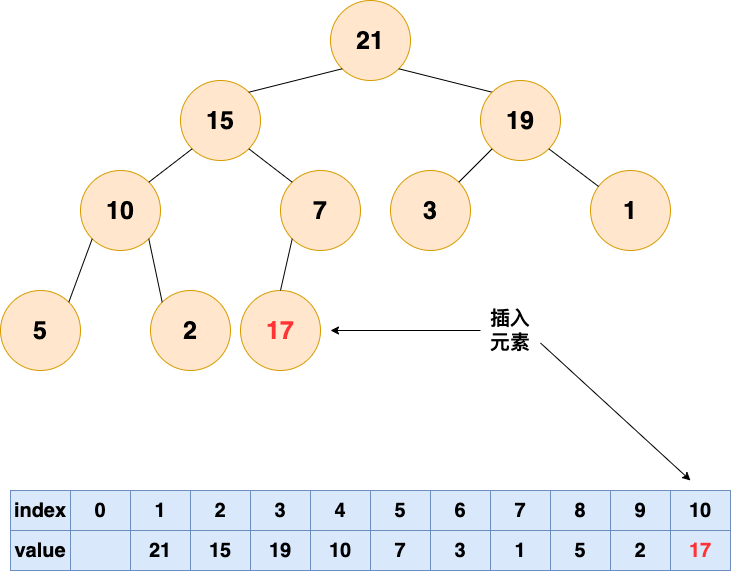
- 将要插入的元素放到数组末尾;
- 自底向上堆化,将末尾元素上浮(如果父结点比该元素大则交换,直到无法交换);
删除堆顶元素
删除(弹出)堆顶元素后,为了保持堆顶元素为最值的性质,需调整堆的结构,称为”堆化“。
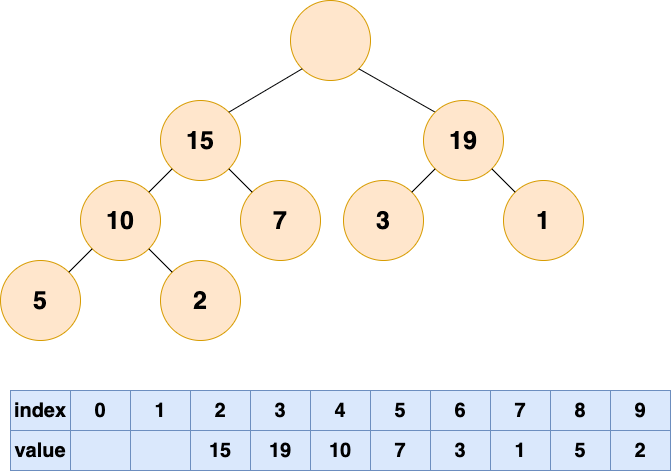
- 自底向上堆化:子节点接力上浮填补空白;易出现“气泡”,导致存储空间浪费。
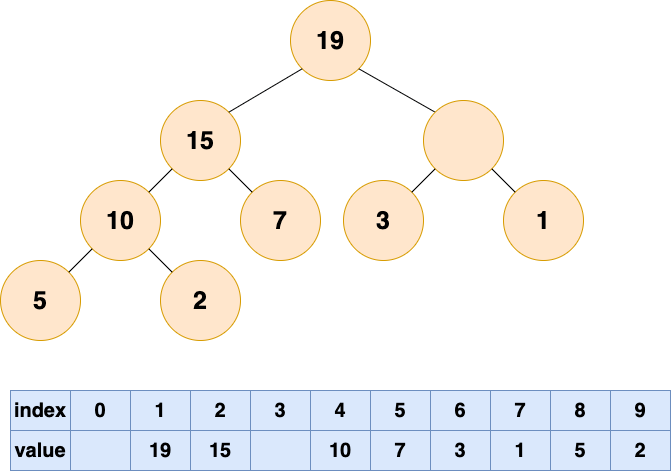
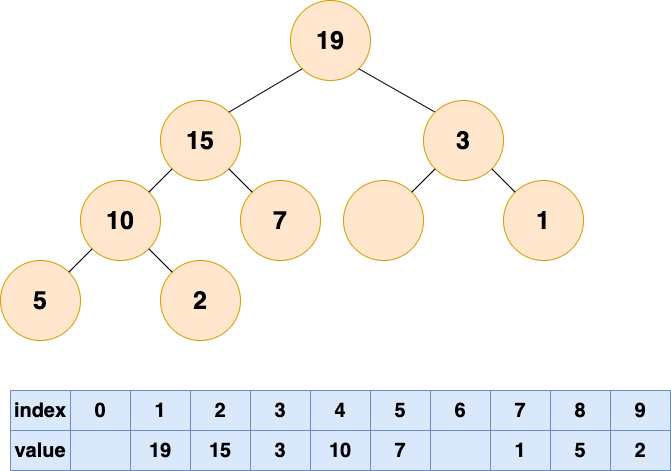
- 自顶向下堆化:不会出现气泡;
- 将末尾元素放至堆顶;
- 堆顶元素下沉(由最顶部向下移动):逐步与左右子节点比较并交换位置,直到无法交换位置;
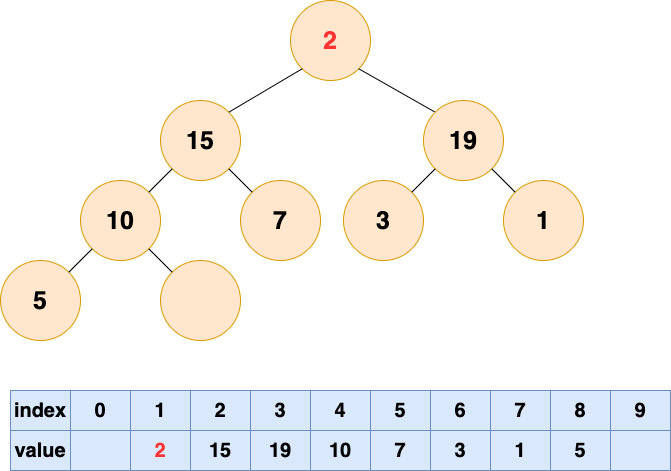
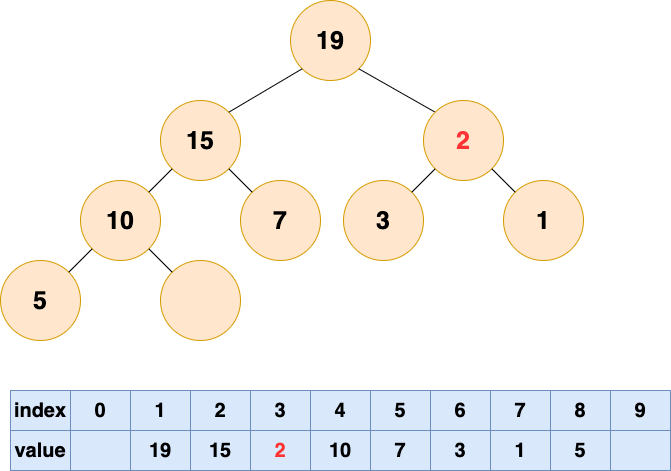
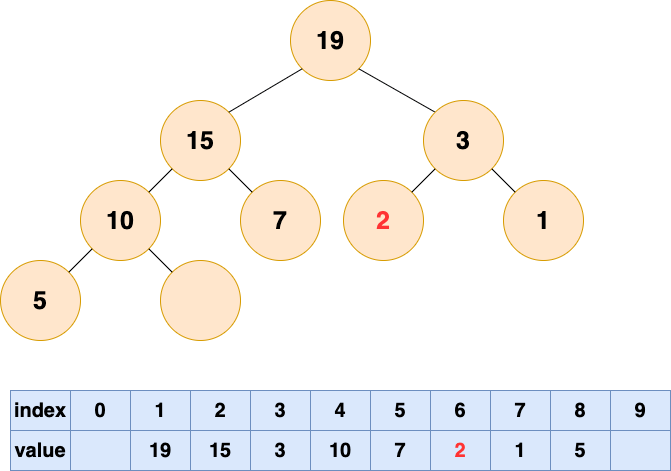
3.2堆排序
第K个元素
-
PriorityQueue:实现大小为k的最小(默认)堆,- 方式一:弹出堆顶的最小元素再加入新元素,重复此过程,始终留下
k个元素(维持堆的大小为k),堆顶(最小元素)即第 k 大的元素;即 [347] 中的思路; 方式二:全部加入堆中,不断弹出堆顶元素,直到剩下k个元素;占用额外空间;
- 方式一:弹出堆顶的最小元素再加入新元素,重复此过程,始终留下
- 方式三:快速选择算法,稍微改造了快速排序的算法思路。【】
-
常规思路:实现最大堆,弹出第 K 个元素;
1
2
3
4
5
6
7
8
9
10
11
12
13// 默认创建最小堆,设置大小为k PriorityQueue<ListNode> pq = new PriorityQueue<>(k, (a, b) -> { return a.val - b.val; }); // 改造为最大堆 PriorityQueue<Integer> pq = new PriorityQueue<>(k, (a, b) -> (b - a)); PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() { @Override public int compare(Integer a, Integer b) { return map.get(a) - map.get(b); } });
-
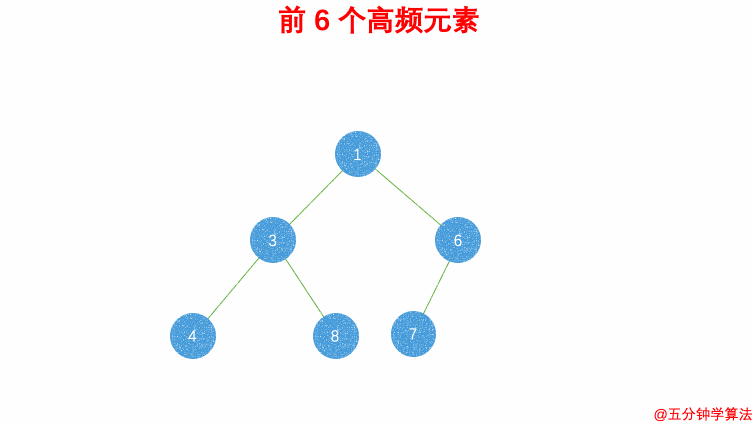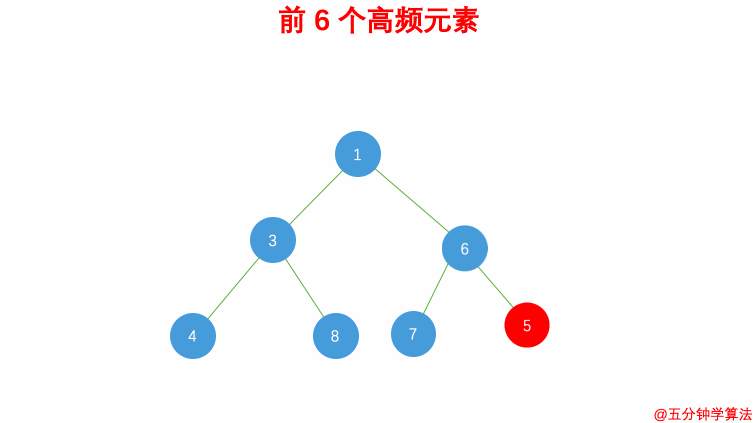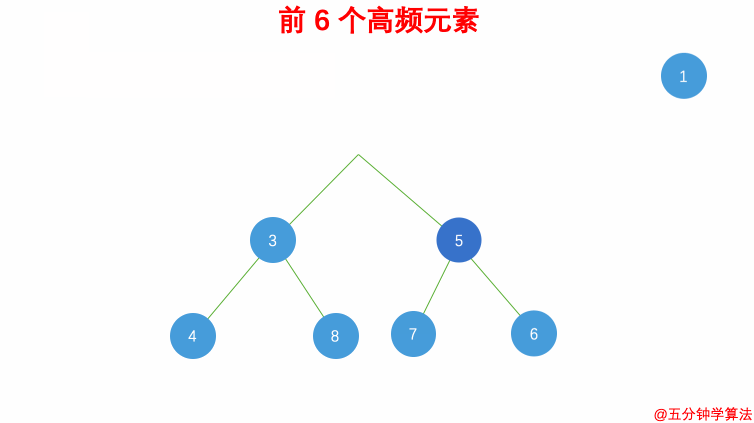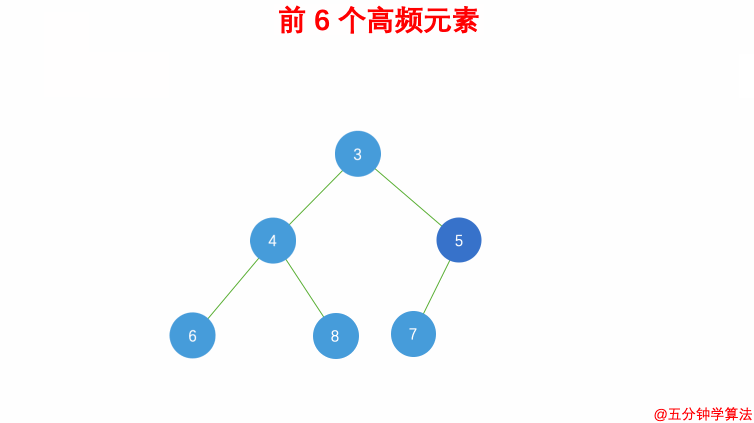
347.前 K 个高频元素:最小堆,借助 哈希表 来建立数字和出现次数的映射,遍历一遍数组统计元素的频率:
- 维护一个元素数目为 k 的最小堆;
- 每次都将新元素与堆顶元素(堆中频率最小的元素)进行比较;
- 如果新元素的频率比堆顶元素大,则弹出堆顶端的元素,将新元素添加进堆中;
-
最终,堆中的 k 个元素即为前 k 个高频元素。
-
23.合并K个升序链表 :将
k条链表的头结点加入最小堆(用PriorityQueue 优先级队列实现)进行节点排序,选取堆顶元素;不断将链表的剩余节点加入最小堆。pq中的元素个数最多是k,一次poll或add方法的时间复杂度是logk;所有节点都会被加入和弹出pq,整体是Nlogk,其中N是所有链表的节点总数。

树
基本概念
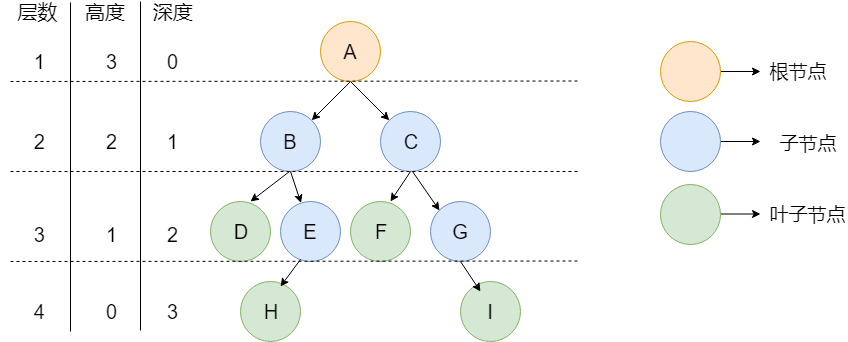
- 节点的高度 :该节点到叶子节点的最长路径所包含的边数;
- 树的高度 :根节点的高度。
- 节点的深度 :根节点到该节点的路径所包含的边数;
- 树的深度:叶子节点的最大深度。
- 节点的层数 :节点的深度+1。
1 | |
树、图的遍历
树的 DFS/BFS 遍历算法
1 | |
经典题目
- 236.二叉树的最近公共祖先
- 递归:根据
root、p、q的关系递归;235.二叉搜索树的最近公共祖先【】 - 还可转化为 两链表的公共节点;
- 递归:根据
Huffman 霍夫曼树
树中的概念:
- 路径:一条从树中任意节点出发,沿父-子节点连接,达到任意节点的通路(序列)。同一节点至多出现一次 ;至少包含一个节点,且不一定经过根节点。
- 路径和:路径中各节点值的总和。
- 单边路径和:从根节点 root 为起点的路径和。
- 路径长度:路径上分支的数目。
- 节点的权:为树中的每一个节点赋予的一个非负的值。
- 节点的带权路径长度:从根节点到该节点之间的路径长度与该节点权的乘积。
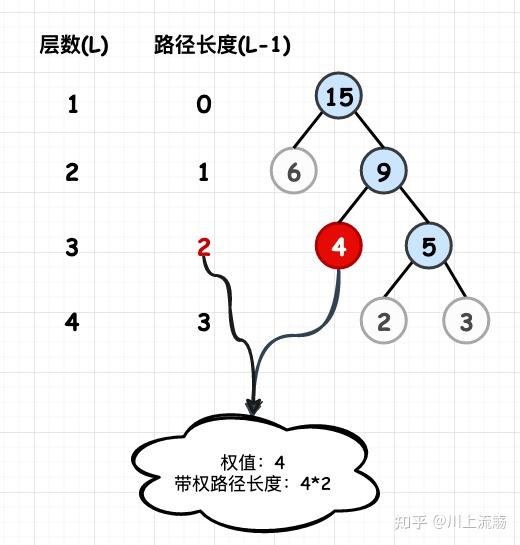
- 树的带权路径长度(Weighted Path Length of Tree,WPL):设二叉树具有 N 个带权叶结点,从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和。
- 所有叶子节点的带权路径长度之和。
Huffman树(霍夫曼树、哈夫曼树、最优二叉树、最优树):在含有 N 个带权叶子结点的二叉树中,其中带权路径长度(WPL)最小的二叉树。
- 哈夫曼树中权越大的叶子离根越近。
- 用途:Huffman编码。
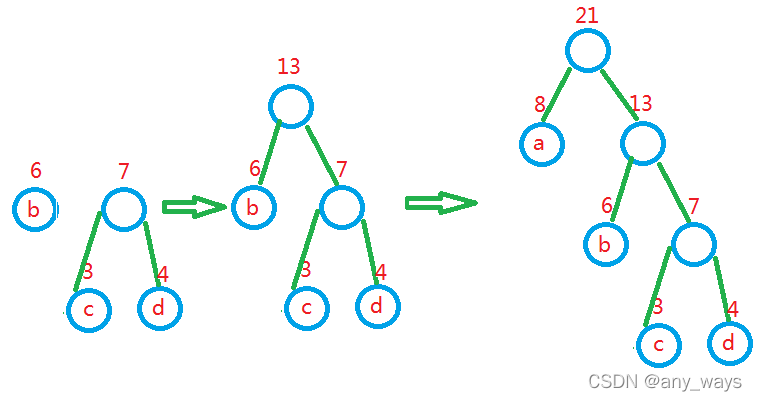
Huffman树的构建
略。
Huffman编码
Huffman编码:由Huffman树生成的二进制前缀编码。
前缀编码:即一个字符的编码不是另一个字符编码的前缀。
二叉树
优点:增删改查性能都很好;
缺点:斜树,瘸子;因此发展出变体满二叉树、完全二叉树。
二叉树核心解题思路
二叉树的习题分为三大部分:
- 递归,用「遍历」的思维模式解题,即 DFS 算法、回溯算法的原型。
- 递归,用「分解问题」的思维模式解题,即动态规划、分治算法的原型。
- 非递归,用「层序遍历」的思维模式解题,即 BFS 算法的原型。
分类
满二叉树、完全二叉树
满二叉树:二叉树每层(第 k 层,深度为 k-1)的结点数都达到最大值 2^(k-1)^,即结点总数是(2^k^) -1。
完全二叉树:最后一层若不满则缺少的节点都在右边,其余层都是满的。性质:父子节点的序号有对应关系。
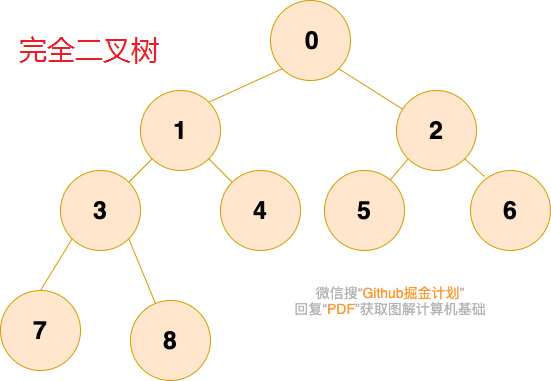
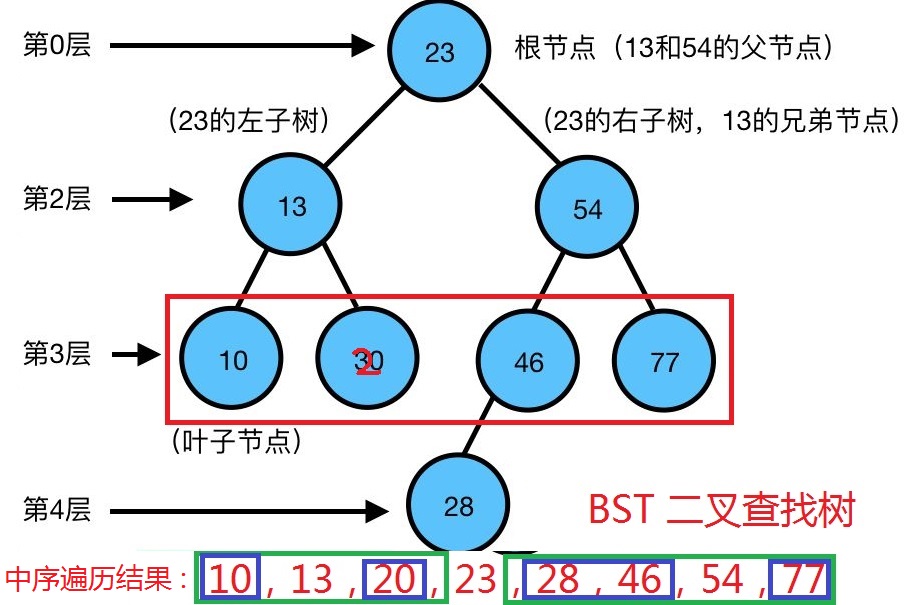
BST 二叉查找树、二叉搜索树
BST 树(Binary Search Tree、ordered binary tree、sorted binary tree):
- (左小右大)若不为空,任意节点的值均 > 左子树任意结点、均 < 右子树任意节点(所有节点的值都不相等),
- 且左右子树都是二叉查找树(即中序遍历为单调递增的二叉树 + 二分查找思想)。
性质:
- 压扁了就是无重复值的有序数组。
由二叉树的层序遍历扩展而来,常用于求无权图的最短路径。维护了一组数据的顺序性,得到一个数据的上下界。 - 查找、插入、删除(CRUD)节点:复杂度均为
O(h+1),h为树的高度/深度,最好(即平衡二叉树)为O(lgN),最坏(斜树)为lgN; - 缺点:若插入的是已有序的序列,可能退化成斜树、链表,CRUD 的性能均从
lgN降为O(N);因此引入平衡二叉树。
经典题目:
- 注意不是所有的 BST 题目都需递归,有的只需
while循环即可; - 108.将升序数组转为高度平衡的二叉搜索树:在前序位置,取
mid位置的元素构造当前root节点,递归创建左右子树;【】- 109.有序链表转换二叉搜索树:链表和数组相比一个关键差异是无法通过索引快速访问元素;【】
- 把链表转化成数组;
- 用双指针获取链表的中点;
- 利用中序遍历的特点写出最优化的解法。
- 109.有序链表转换二叉搜索树:链表和数组相比一个关键差异是无法通过索引快速访问元素;【】
AVL 平衡二叉树、红黑树
平衡二叉树、AVL 树():除了空树,每个节点的左右子树都是一棵平衡二叉树、且高度差的绝对值不超过1。常用实现方法有 红黑树、替罪羊树、加权平衡树、伸展树 等。
红黑树(自平衡二叉查找树、对称二叉 B 树):一篇漫画告诉你–什么是红黑树?
- 一种二叉查找树,满足:
- 根、所有叶子节点(为空、
NIL/null)都是黑色; - 每个红节点必须有两个黑子节点。即:
- 红节点的父、子节点均是黑色;
- 从每个叶子到根的所有路径上不能有两个连续的红节点;
- 不存在两个相邻(父子关系)的红节点;
- 从任一节点到每个叶子的所有简单路径都包含相同数目的黑节点。确保没有一条路径会比其他路径长出两倍。
- 根、所有叶子节点(为空、
- 既有线性表的二分查找、有序,又有链表的增删性能。可在
O(lgN)时间内完成查找、插入和删除。 - 典型用途是实现关联数组,
TreeMap、TreeSet及JDK1.8的HashMap底层都用到红黑树。 - 变色:添加、删除;
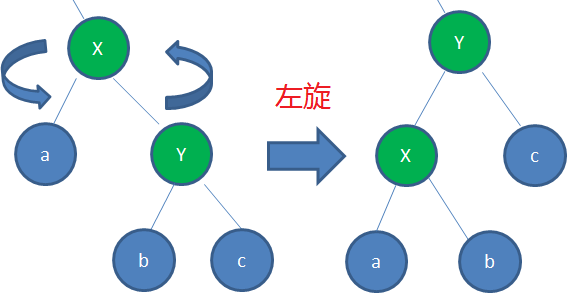
-
左旋算法:父节点被自己的右孩子取代。

B 树 / 多路平衡查找树
B+ 树(B 树的变形):用于数据库索引的实现。是一种红黑树,也是一种 BST 二分查找树?
B 树 VS B+ 树:
- 节点:
B树的所有节点存放键和数据,而B+树只有叶子节点存放key和data,其他非叶子节点只存放key。 - 叶子节点:
B树的叶子节点是独立的;B+树的叶子节点有引用链指向相邻的叶子节点。 - 查找:
B树的检索相当于对节点的关键字做二分查找,可能不到叶子节点就找到;而B+树的查找是从根节点到叶子节点。
其他二叉树
Trie树、字典树、前缀树、单词查找树:由二叉树衍生出来,主要用于处理字符串前缀相关的操作、保存和统计大量的字符串和相关的信息。-
线段树:叶子节点是数组中的元素,非叶子节点就是索引区间(线段)的汇总信息。用于高效解决数组的区间查询和区间动态修改问题。如处理数组区间信息的汇总(求和、最值等)、单点更新、区间更新问题。
- 树状数组:处理数组的前缀和、单点更新、区间更新问题。
二叉树的存储
- 链式存储
-
顺序存储:用于堆的存储;
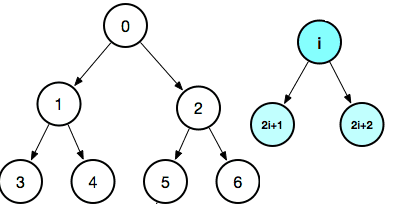
- 根结点的序号为 0,则下标为
i的节点对应的:- 父结点:
(i - 1) / 2 - 左子结点:
2 * i + 1 - 右子结点:
2 * i + 2 - 非叶节点:
[0, (n-1)/2],用于建堆;
- 父结点:
- 根结点的序号为 1,对于树中任意节点
i,其- 父结点:
i / 2 - 左子节点序号为:
2 * i - 右子节点为:
2 * i + 1
- 父结点:
- 根结点的序号为 0,则下标为
代码实现
1 | |
二叉树遍历
层序遍历
外部变量 + 迭代遍历一遍:对应回溯算法核心框架,简单易懂;
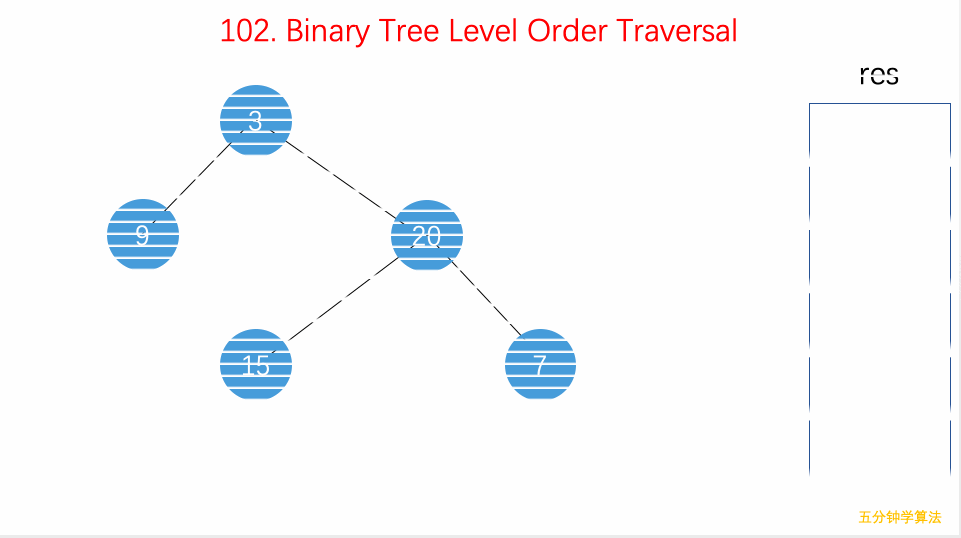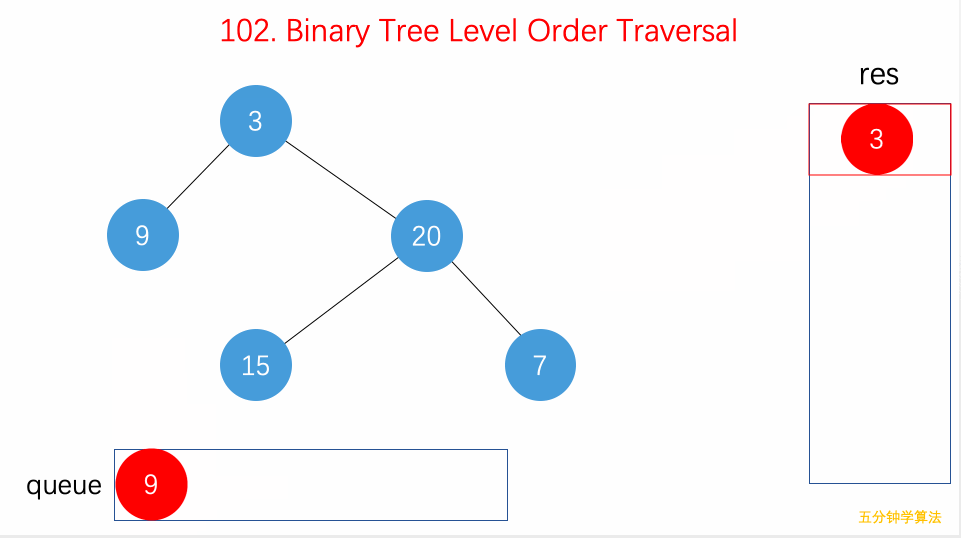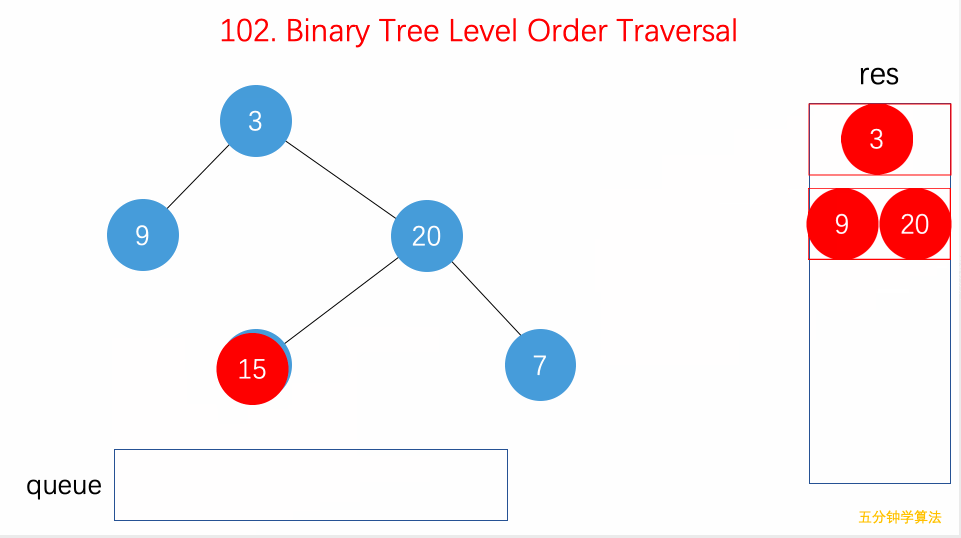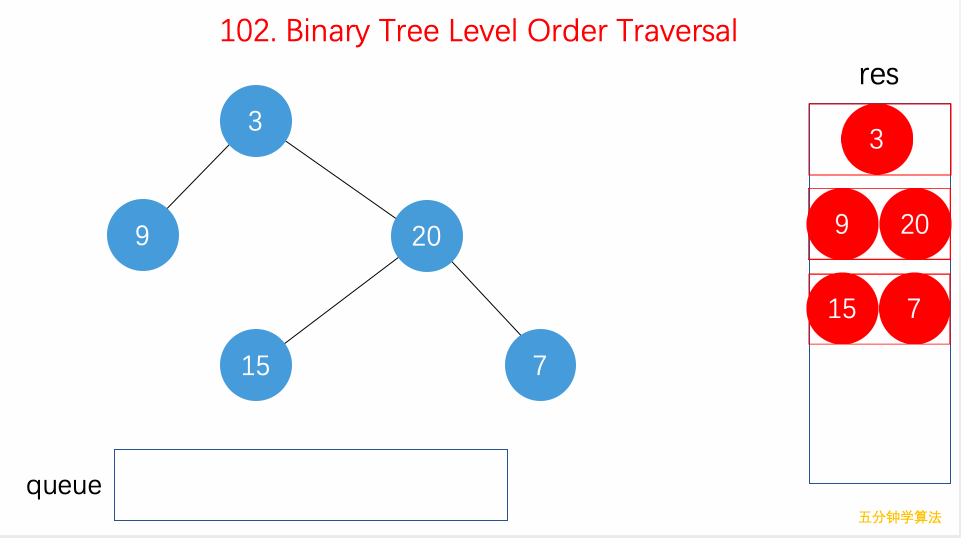
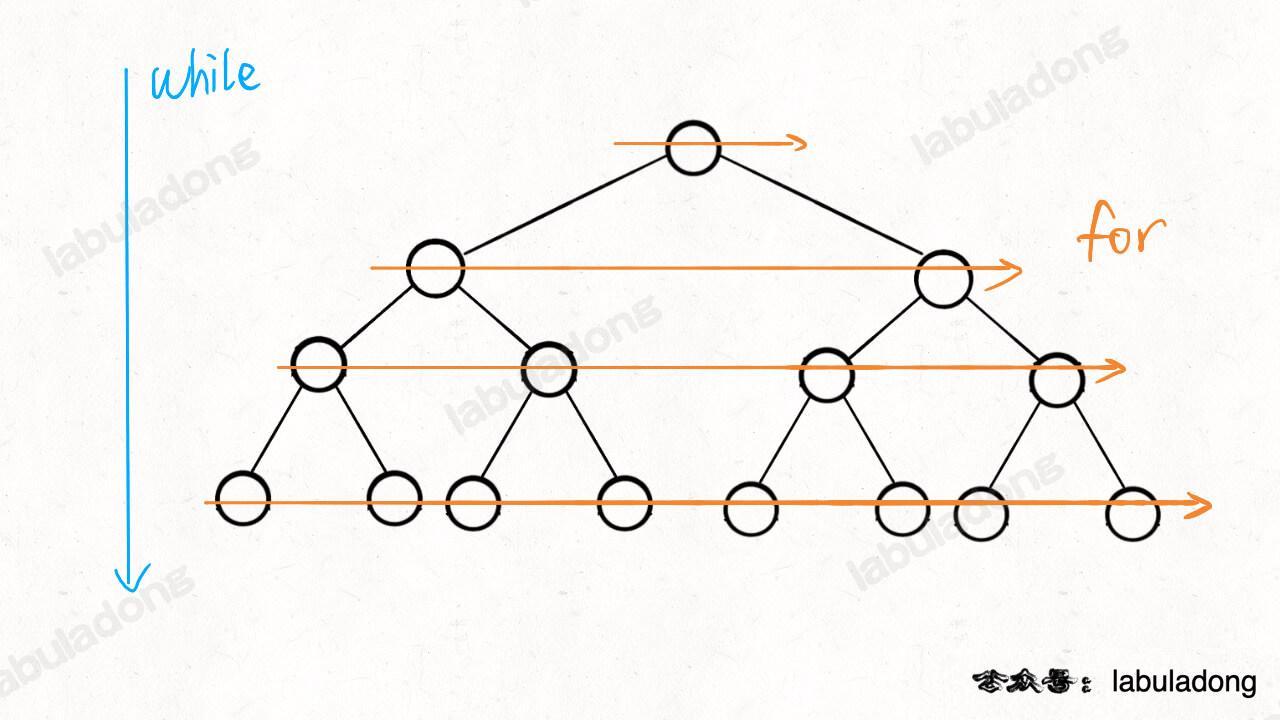
- 102.二叉树的层序遍历:从上到下用
while遍历每层、并塞入队列,自左向右用for遍历每行、将结果加入 List。可扩展出 BFS 算法框架; - 111.二叉树的最小深度
- 103.二叉树的锯齿形层序遍历:奇偶层
ArrayList分别用addLast()、addFirst();【】 - 107.二叉树的自底向上层序遍历 II【】
- 从上到下打印每行中的最大值;
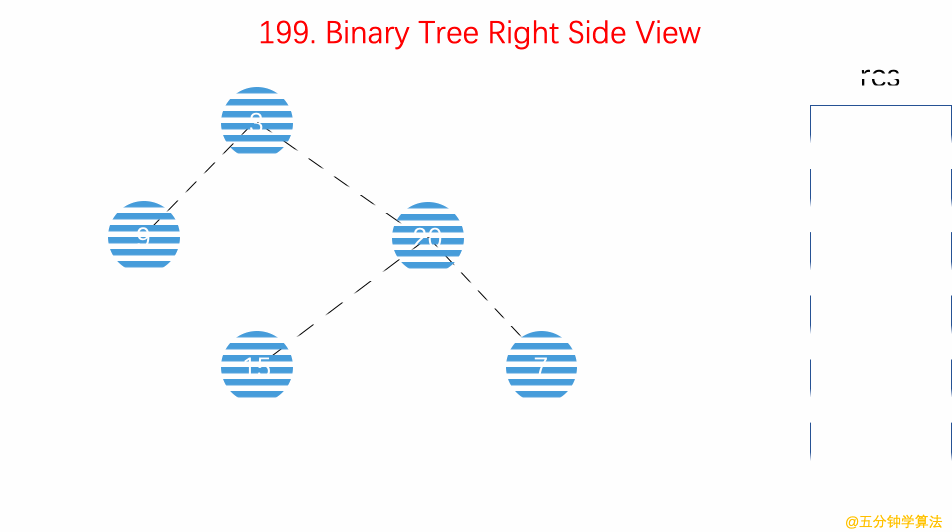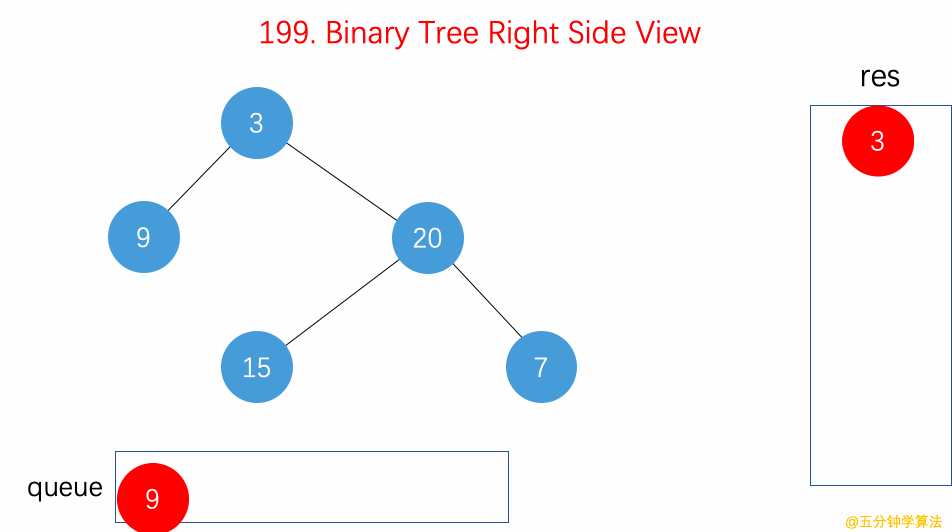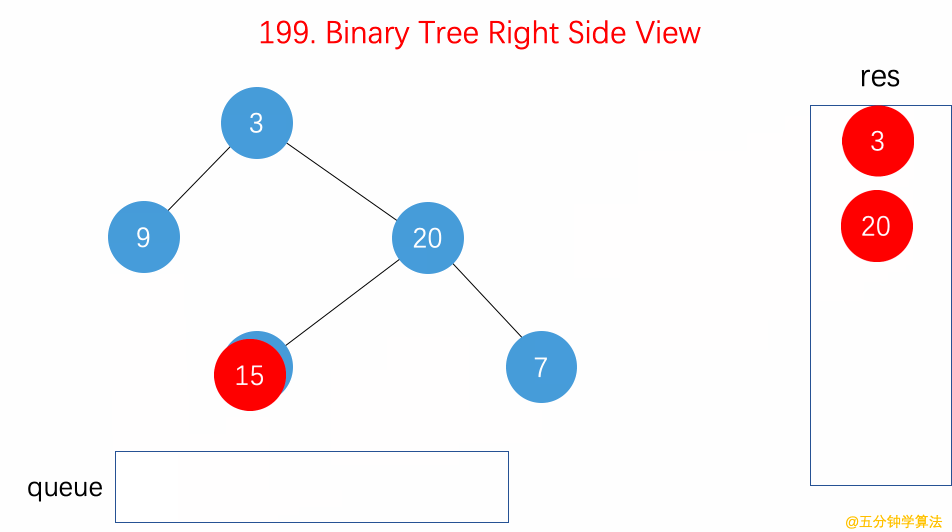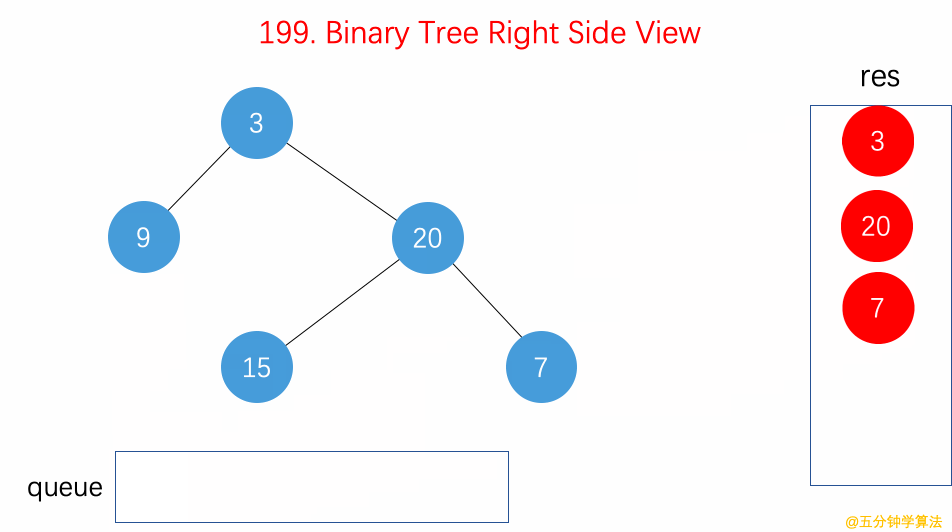
- 199.二叉树的右视图【】
- 用 BFS 层序遍历算法,从右往左遍历每行,每层
queue的第一个节点就是右视图。 - 用 DFS
递归遍历算法,反过来从右往左遍历每一行,先递归root.right再递归root.left,同时用res记录每层的最右侧节点作为右视图。
- 用 BFS 层序遍历算法,从右往左遍历每行,每层
- 103.二叉树的锯齿形层序遍历:奇偶层
层序遍历框架:
1 | |
前序/中序/后序遍历
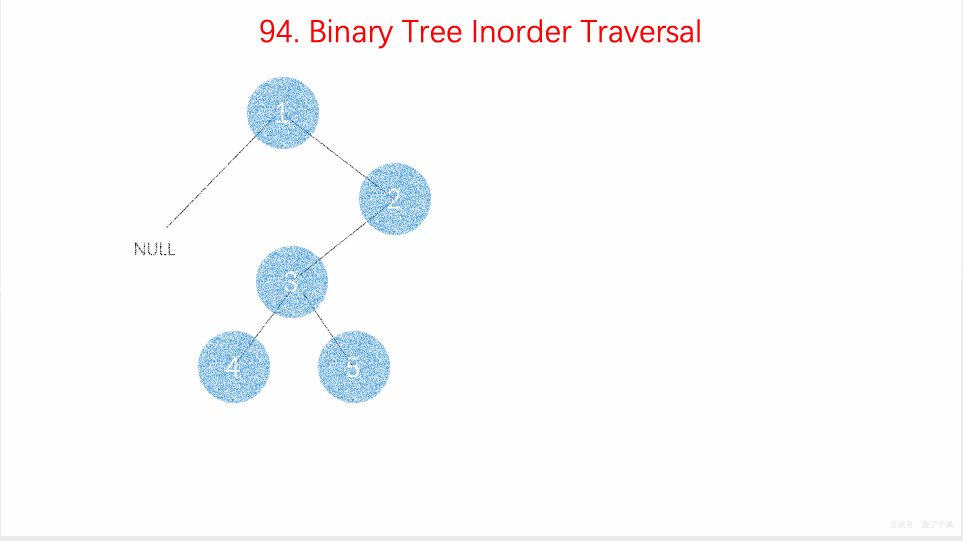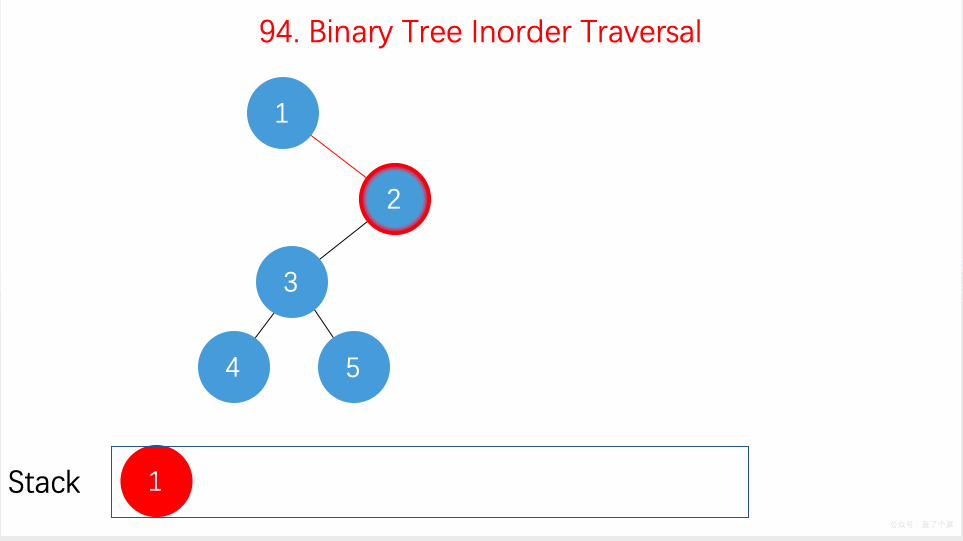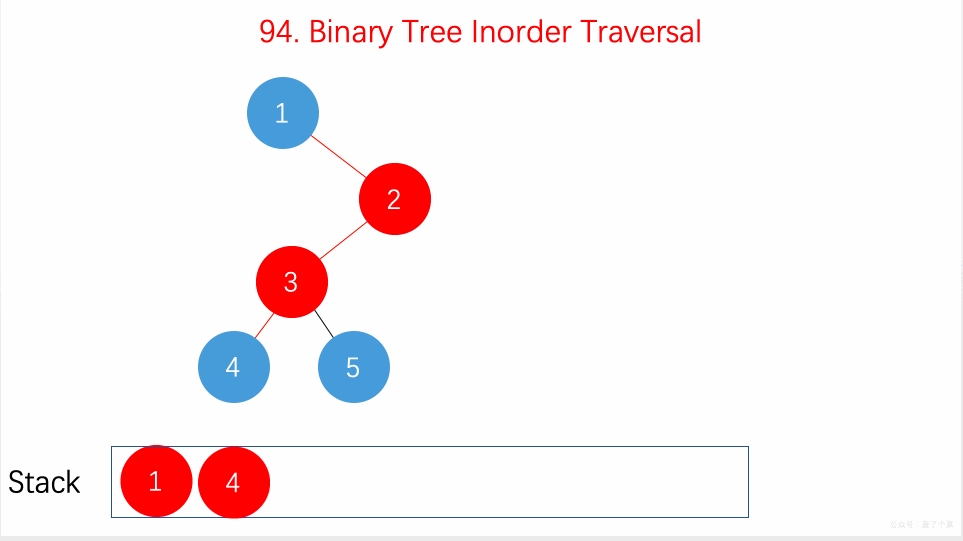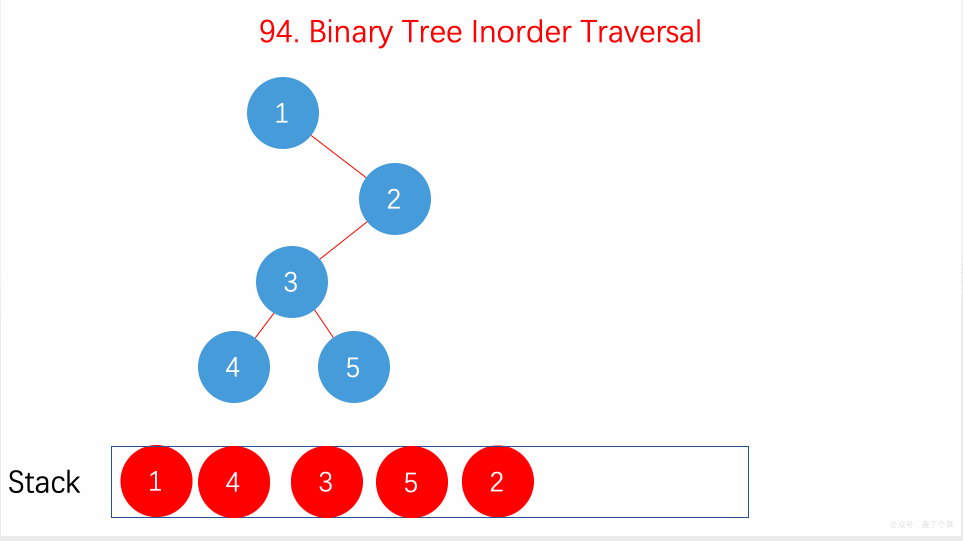
- 144.二叉树的前序遍历:逻辑上用栈,实际在递归的前序位置用递归栈;
- 94.二叉树的中序遍历:在递归的中序位置用递归栈、不用递归;【】
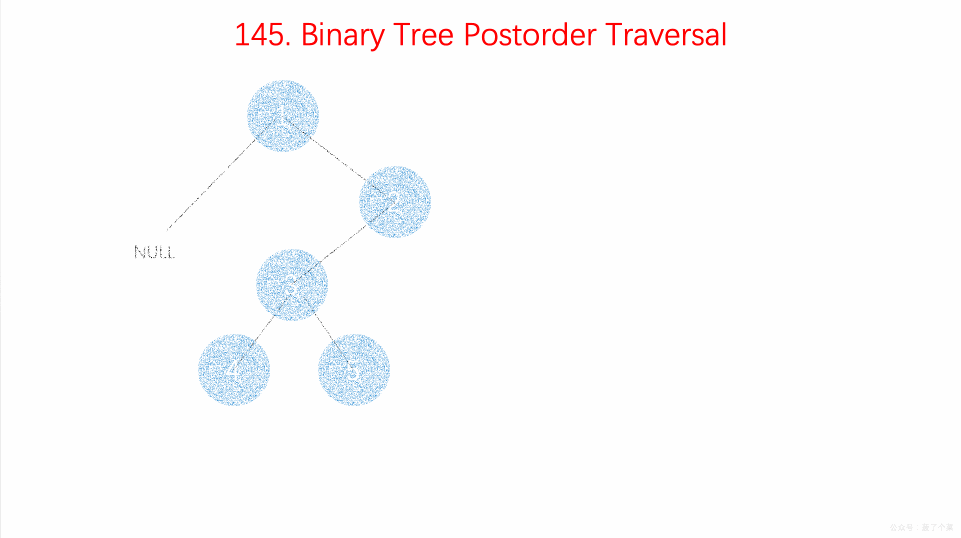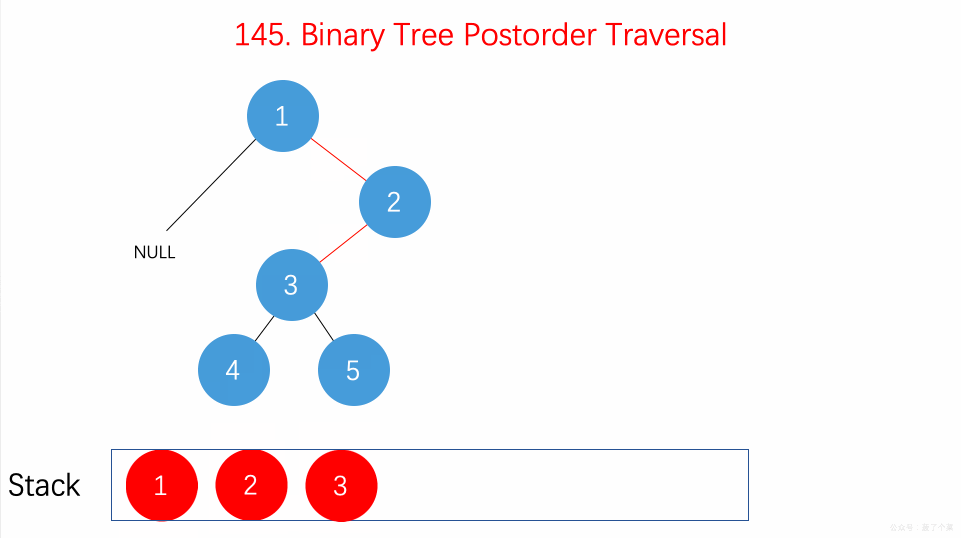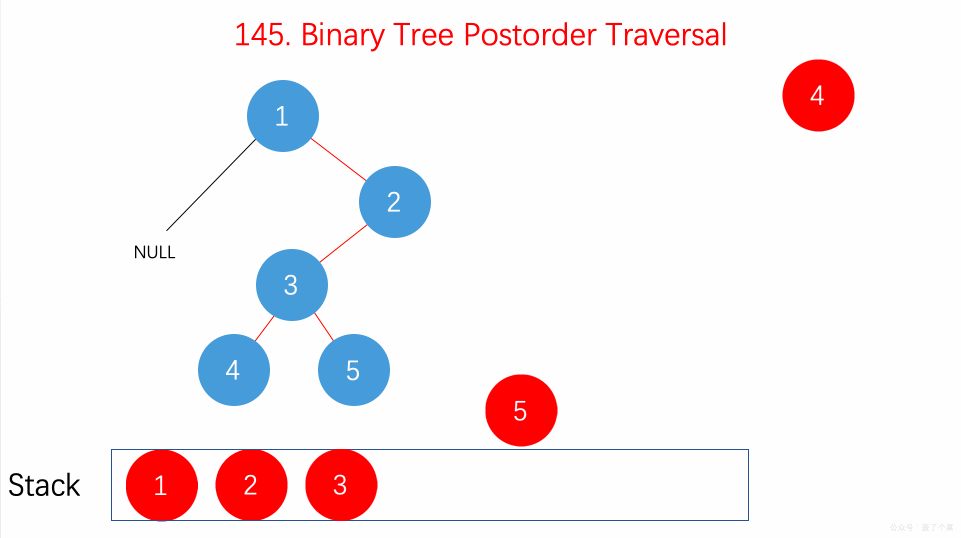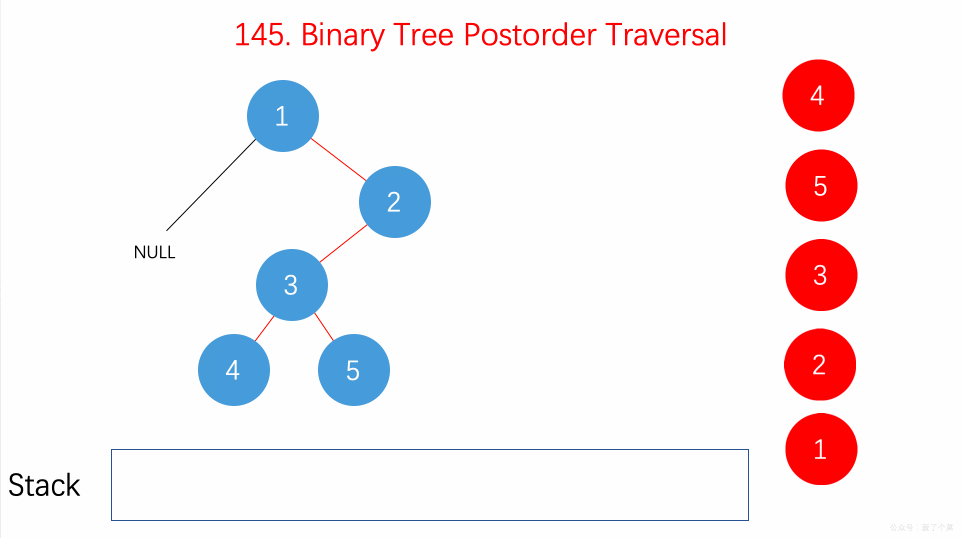
- 145.二叉树的后序遍历:在递归的后序位置用递归栈;【】
-
124.二叉树中的最大路径和:递归后序遍历时,计算单边路径和、最大路径和【】
-
-
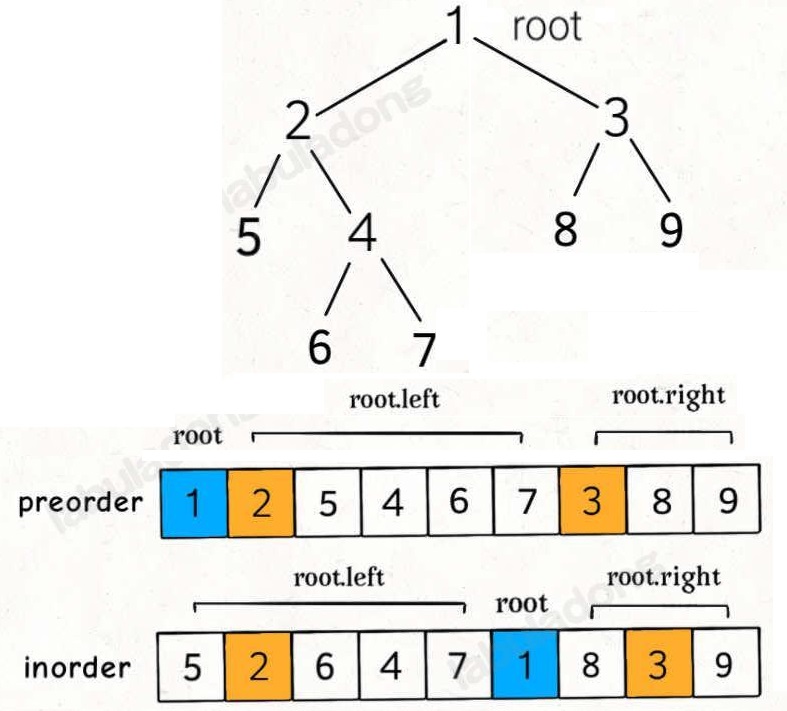
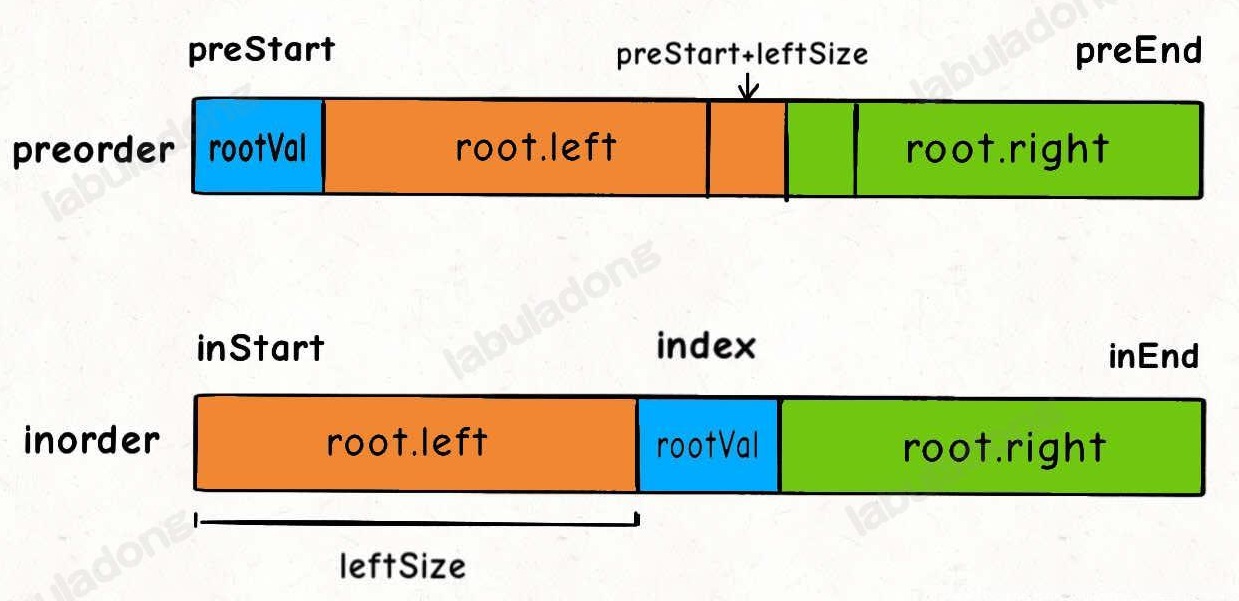
105.根据前序与中序遍历序列构造二叉树:
inorderValToIdxMap<>存储中序序列的值到索引的映射;前序序列preorder[preStart, preEnd]确定 root 、左子树 + 右子树的范围,再根据中序序列inorder[inStart, inEnd]确定(划分)左右子树的长度,得到左右子树的前序和中序序列,递归;
递归框架:
在递归函数中,将当前节点分解为子问题(子树),通过子树的结果推导出当前节点的结果:对应动态规划核心框架;
1 | |
(非递归不用栈的)中序遍历
用循环/迭代、中序遍历。
利用线索二叉树的思想,即不再闲置叶子节点的左右指针,比如中序利用叶子节点右指针指向前序遍历情况时的后继节点。在当前节点没有左子树、或者第二次访问节点时即为中序结果。
- 此时past的右孩子指向后继节点,所以是第二次访问;
- 代表当前结点的左子树已经访问完毕,所以访问当前结点;
- 然后把指针移到后继或者右子树,并消除多余链接;
递归和迭代两种方式是等价的,区别在于递归的时候隐式地维护了一个栈,而在迭代时需要显式地将这个栈模拟出来。
参考:二叉树遍历四种必会算法:递归遍历、非递归遍历、既不用递归也不用栈遍历(三种深度优先),层序遍历(广度优先)
难理解,直接背。
1 | |
经典题目
图
面试笔试很少出现图相关的问题,就算有大多也是简单的遍历问题,基本上可完全照搬多叉树的遍历。
基本概念
图(G)由顶点的有穷非空集合(V)和顶点间的边(E)组成,通常表示为:G(V,E)。如社交软件上好友关系。
- 无向图和有向图;
- 无权图和带权图;
树和图的根本区别:树不含环,图可能含环。树是一种图,即无环连通图,图是多叉树的延伸。如果图没有环,可拉伸成一棵树。
- 度(degree):每个节点相连的边数。
- 入度(indegree):有向图中指向每个节点的边数;
- 出度(outdegree):有向图中从每个节点出发的边数。
用途:
- 哈希环:用于负载均衡算法中的一致性哈希法。
图的存储
表示方法、具体实现、物理结构
-
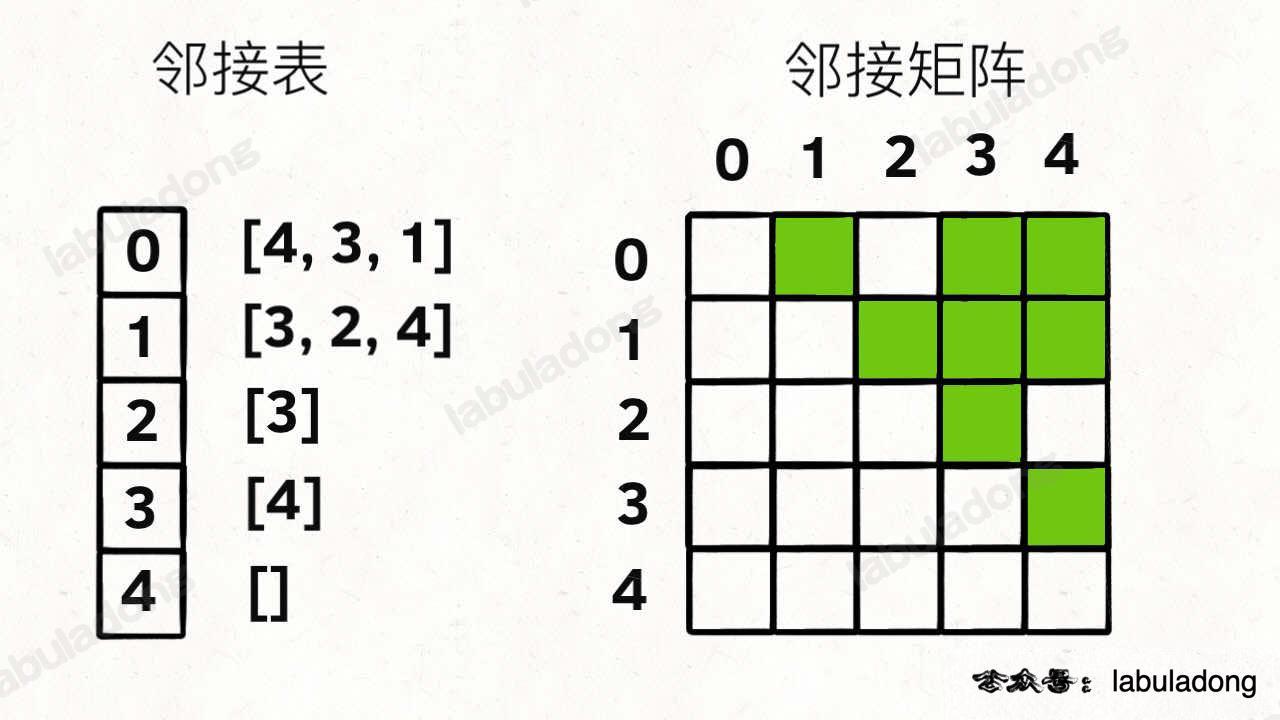
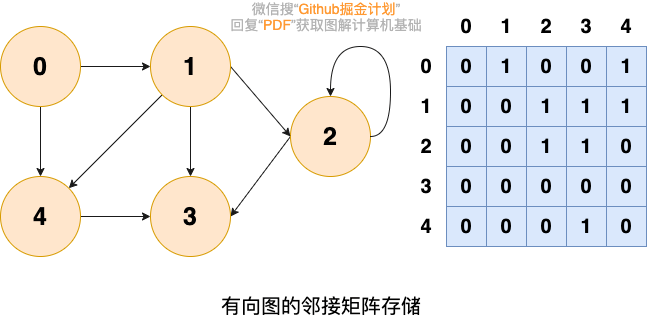
邻接矩阵:优点是简单直接(用一个二维数组),可快速判断两点间是否连通,可进行矩阵运算,但(图比较稀疏时)会浪费空间。
-
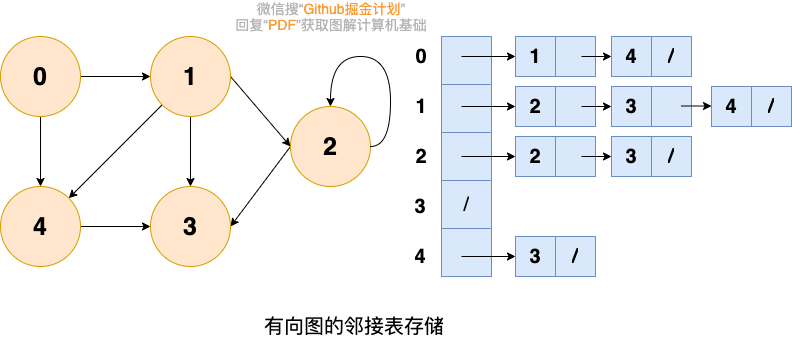
邻接表:比较节省空间,但很多操作效率低,如无法快速判断两个节点是否连通。在常规的算法题中使用更频繁。
- 在无向图中,邻接表元素个数等于边数的两倍;
- 在有向图中,邻接表元素个数等于边的条数;
1 | |
图的搜索、遍历
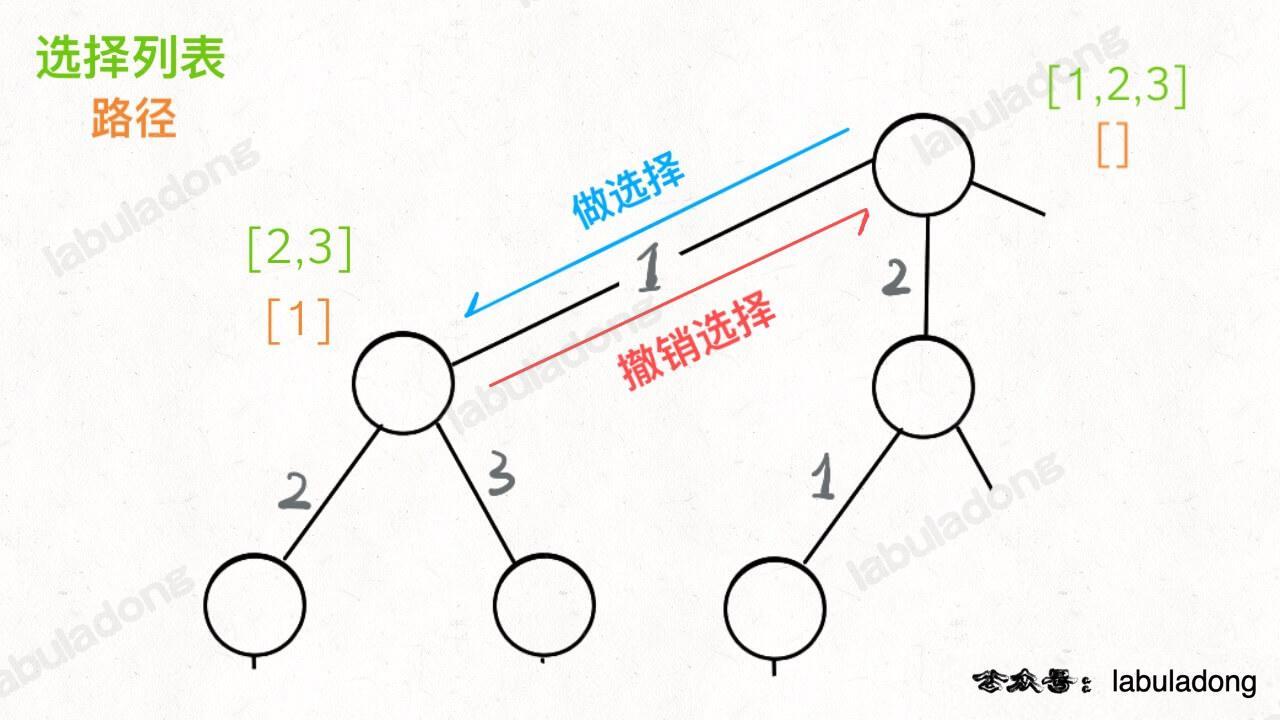
各种搜索问题其实都是树的遍历问题:
- DFS 深度优先搜索:用栈回溯;
- BFS 广度优先搜索:把问题抽象成图,每次将当前节点周围的所有节点加入队列。
二者最主要的区别是:
- BFS 的
depth每增加一次,队列中的所有节点都向前迈一步,保证了第一次到达终点时,走的步数是最少的,可在不遍历完整棵树的条件下找到最短路径。 - DFS 实际上是靠递归的堆栈记录走过的路径,把二叉树中所有节点都走完才能对比出最短路径。
BFS 空间复杂度比 DFS 大。
1 | |
1 | |
Kruskal 最小生成树算法
经典算法,学有余力可以掌握一下
图的生成树:生成树是包含图中所有顶点的无环连通子图(无环树)。
最小生成树(MST):权重和最小的生成树。都用了贪心思想。1584.连接所有点的最小费用【】
Kruskal克鲁斯卡尔算法:用到了贪心思想,使权重和尽可能小。对所有边按照权重从小到大排序,从权重最小的边开始,选择合适的边加入mst集合;如果边的两端点不属于同一集合,则合并,直到所有的点都属于同一个集合为止。实就是 Union Find 算法 + 排序。用并查集算法来保证生成树不含环且不是森林:- 如果一条边的两个节点是连通的,则会出现环;
- 如果最后的连通分量总数大于 1,则说明是「森林」。
- 并查集 Union-Find Disjoin Sets(UFDS):用于处理不相交集合的动态连接问题。模拟多个不相交集,能在几乎常数时间内确定一个元素属于哪个集、测试两个元素是否属于同一个集、将两个不相交集合并为一个。在
Kruskal算法中用来寻找无向图中的连接分量。
Prim普瑞姆算法:核心是切分定理(将图分为两个不重叠且非空的节点集合),每次都把权重最小的「横切边」拿出来,直到把构成最小生成树的所有边都切出来为止。用 BFS 算法思想 和visited布尔数组避免成环。
Dijkstra 最短路径算法
,经典算法,学有余力可以掌握一下。
简单图(有向无向皆可)的最短路径 Dijkstra 迪杰斯特拉(戴克斯特拉)算法:注意是长度而不是具体的路径。是 BFS 算法的加强版,都是从二叉树的层序遍历衍生出来。
- 用于计算 OSPF 动态路由选择协议。
经典题目
- 看到依赖问题 ==> 首先想到的就是把问题转化成「有向图」
比较基本且有用的算法,应较熟练地掌握:
-
有向图的环路检测、循环依赖判断:207.课程表 选修依赖先修【】、二分图判定算法,常用邻接表,DFS 算法遍历图的框架 +
visited数组- DFS 实现
- BFS 实现
-
拓扑排序(Topological Sorting):是一个有向无环图所有顶点的线性序列;
- 每个顶点出现且只出现一次;
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
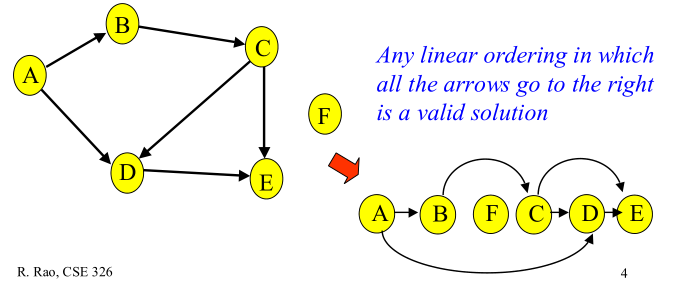
-
直观说就是,把一幅图「拉平」,且所有箭头方向都是一致的。存在环,则肯定做不到所有箭头方向一致。如返回一个合理的上课顺序,保证开始修每个课程时,前置课程都已修完。实现:
- DFS 实现(可进一步理解递归)
- BFS 实现(更简洁)
-
二分图的判定、图论的双色问题:二分图的顶点集可分割为两个互不相交的子集,图中每条边依附的两个顶点都分属于这两个子集,且两个子集内的顶点不相邻。
-
Union Find 算法:
Kruskal克鲁斯卡尔算法,最小生成树。- 使用并查集操作联通分量。