摘要:手撕算法多为框架,包括常用技巧、十大排序算法、查找、分治与递归、动态规划、贪心、BFS 框架、DFS框架与回溯、缓存淘汰算法。基本涵盖labuladong 的算法小抄、CodeTop频度前40、剑指 Offer(第 2 版)、LeetCode 热题 HOT 100常见例题。
目录
[TOC]
手撕算法
算法定义
- 数据结构:是解决问题的过程中(存放、处理数据)的容器和缓存,是空间换时间思想的体现。
- 算法:是(正确、高效)解决问题的方法:
- 算法工程师(数学算法):重点在数学建模和调参经验,计算机只是拿来做计算的工具而已;
- 数据结构与算法(计算机算法):重点是计算机思维,站在计算机的视角,抽象、化简实际问题,用合理的数据结构去解决问题。
大部分开发岗位工作中都是基于现成的开发框架做事,不怎么会碰到底层数据结构和算法相关的问题,但技术相关的岗位,数据结构和算法的考察,公认的程序员基本功。
常用技巧
一题多解、多题一解。一句话题解、写题目详解、写总结。
- 排序类
- 数组、字符串:二分查找
- 单链表:
- 子串:快慢双指针(滑动窗口)
- 反转链表
- 三大牛逼算法:回溯、贪心、动态规划(DP)
- 递归类:
- 二叉树:
- 回溯算法核心框架:遍历一遍二叉树得出答案;
- 动态规划核心框架:通过分解问题计算出答案;
- 二叉树:
- 非递归类:无遗漏(正确不出错)、无冗余(优化算法的时间、空间复杂度)聪明的穷举。
- 贪心:在题目中发现一些规律(专业点叫贪心选择性质),不用完整穷举所有解。
- 递归类:
- 分治:核心依然是大问题分解成子问题,只不过没有重叠子问题
时间、空间复杂度
分析算法复杂度时,分析的是最坏情况的复杂度。
O(1)、O(n)、O(lgN)。
- 时间复杂度用来衡量一个算法的执行效率,
- 空间复杂度用来衡量算法的内存消耗。
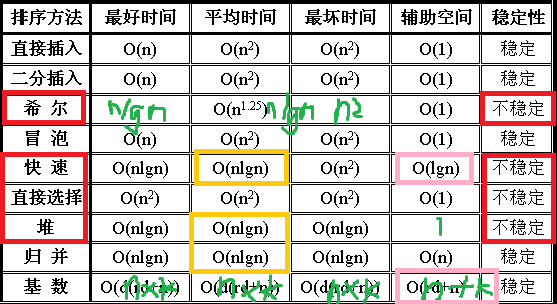
排序
排序算法总结和比较。注意写代码的流畅度。
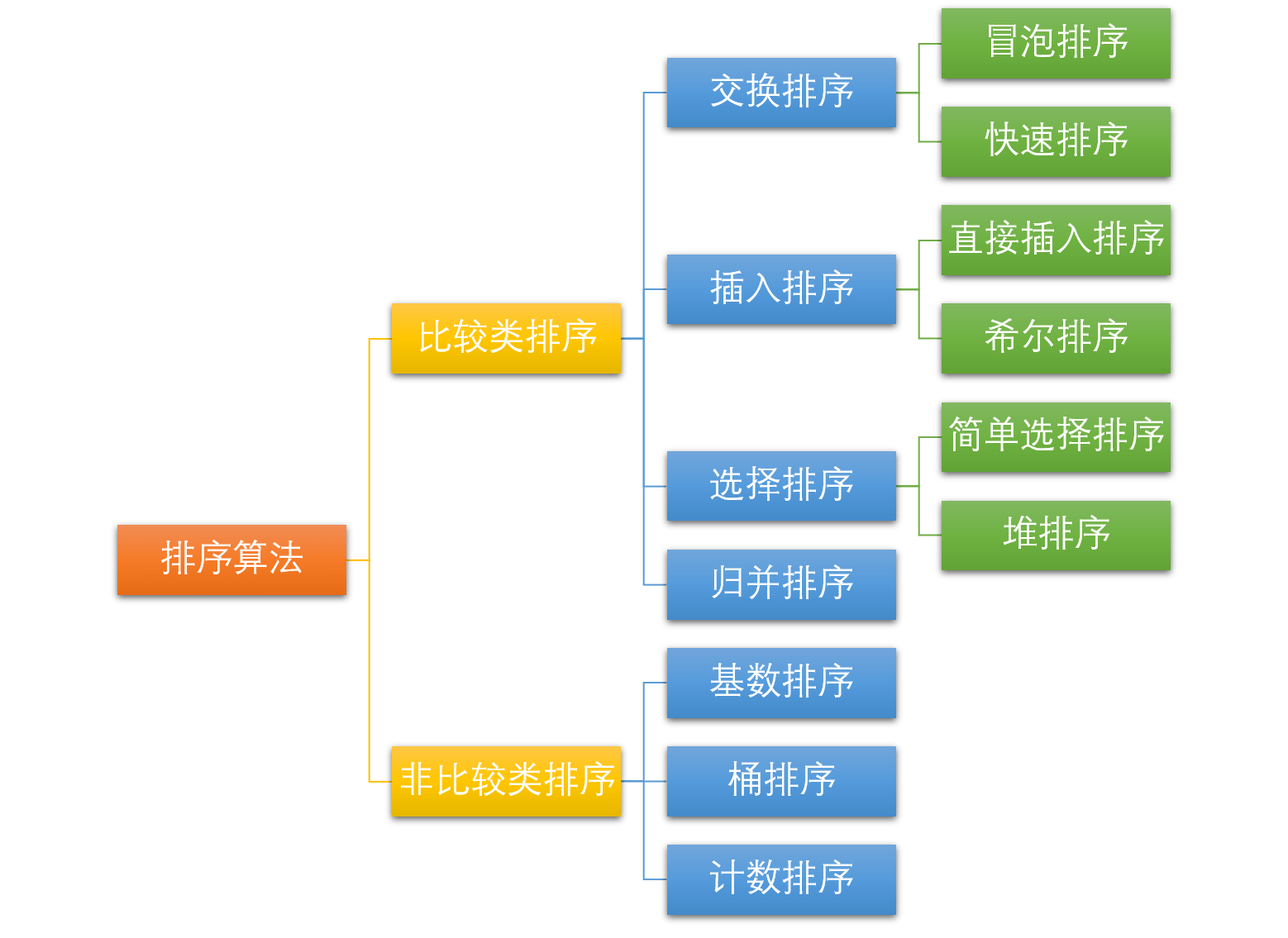
可分为:
-
内部排序:数据记录在内存中进行排序;
- 比较类排序:通过比较元素大小来排序;
-
非比较类排序(线性时间):不通过比较、而是通过每个元素前的元素个数来排序(决定元素间的相对次序);
- 一次遍历即可,可突破基于比较排序的时间下界,以线性时间运行,算法时间复杂度
O(n); - 以空间换时间:需占用空间来确定唯一位置,对数据规模和分布有一定要求。
- 一次遍历即可,可突破基于比较排序的时间下界,以线性时间运行,算法时间复杂度
-
外部排序:数据量很大,内存一次不能容纳全部记录,需访问外部文件(外存)。
稳定性:相同的值经过排序后、相对次序保持不变。
-
四个不稳定的算法:希快选堆(1.2、2.2、3.1、3.2)。
-
可能变为不稳定:插冒(1.1、2.1)。
0. 内置排序函数
1 | |
1. 插入排序
1.1 插入排序
- 工作原理:(将待排序元素)分为已排序和未排序两部分。相当于抓牌 + 插牌的过程:
- 抓牌:遍历未排序元素,作为待插入元素;
- 插牌:
- 直接插入:由后向前查找当前元素在已排序元素中的插入位置,将后面的元素逐个后移,插入目标位置;
- 折半插入:二分查找插入位置(右边界),统一后移。
- 最易理解
- 性能/复杂度:
n(有序、设置flag表示此趟是否排序)、n^2^、n^2^(逆序)、O(1)。 - 稳定:查找右边界(值相等就停止向前查找)时,值相等的元素保持原来的相对位置(原序)。
1 | |
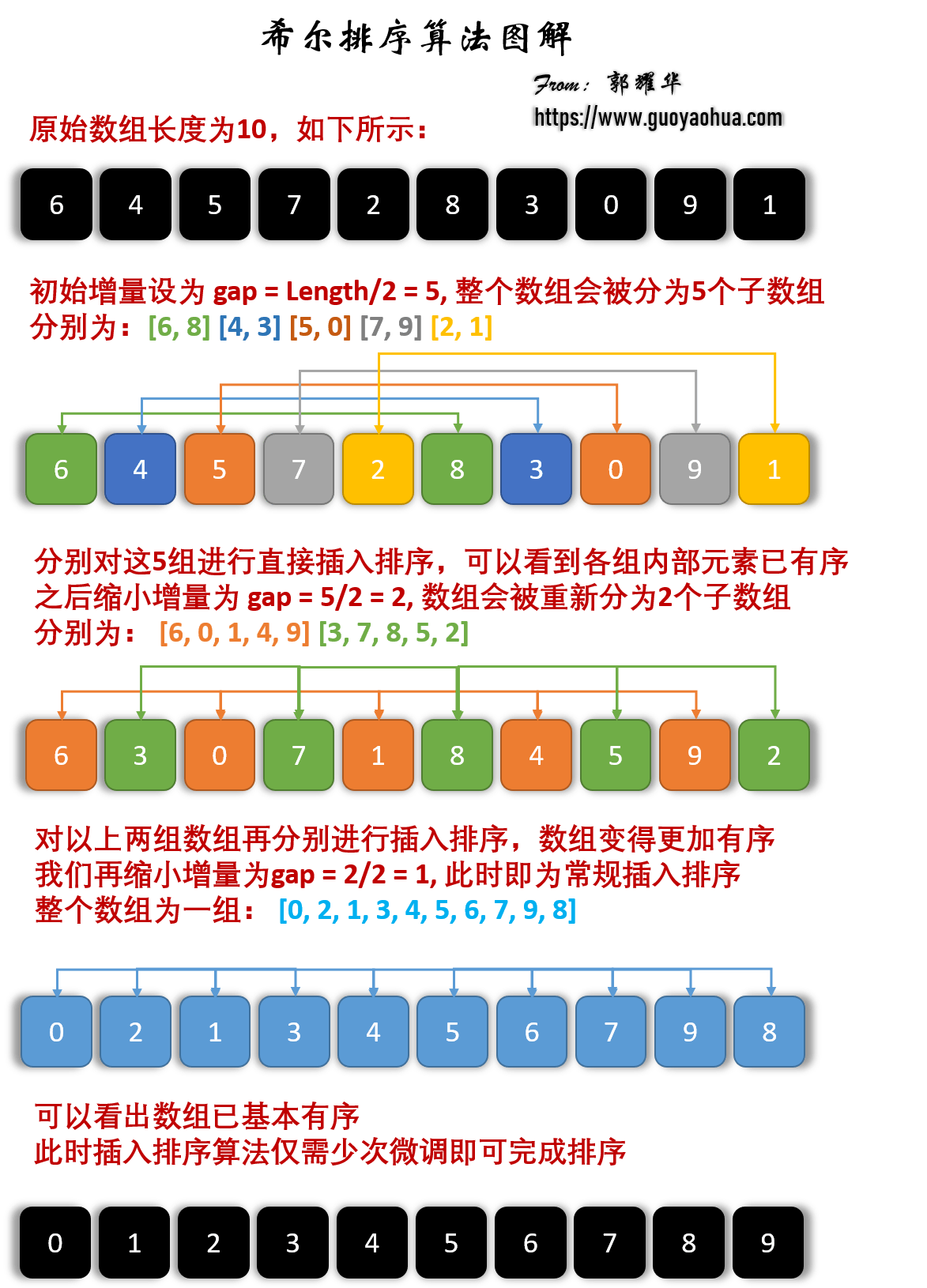
1.2 希尔排序
- 又称缩小增量排序;
-
基本思想:
- 将整个待排序的记录,分成为若干组子序列,在组内(直接插入)排序;当整个序列中的记录基本有序时,再对全体记录排序;
- 间隔为步长(倍数)的位置分为一组(物理上并不相邻,逻辑上通过步长相邻),组内直接插入排序,不断缩小步长,通常步长减半
gap[i]:n/2 -> 1(步长为 1 即直接插入排序)。
- 复杂度:根据实现方式有所区别,一般认为
nlogn、nlogn?、n^2^、O(n)。 - 不稳定:同组内元素交换位置后,不同组内相等元素的相对位置可能改变。如
[2, 2, 1, 3]。
1 | |
2. 交换排序
2.1 冒泡排序
- 基本思想:在未排序序列
[0,n-i)范围内冒泡一次,相邻元素两两排序(逆序则交换)作为一趟冒泡,即最大的元素向后冒泡,加入已排序元素的左侧。注意 i、j 的起始取值。 - 性能:
n、n^2^、n^2^、O(1)。 - 稳定:交换时,元素相等就停止交换,可保证相对位置不变;(若改成
arr[j-1] >= arr[j]),两个相等的记录就会交换位置,则变为不稳定。
1 | |
2.2 快速排序
- 又称分区交换排序。
- 基本思想:选取一个基准元素
pivot(即划分标杆、枢纽、比较子),通过一趟划分(分治法)将序列分隔成两个子序列:比基准元素小的元素都放在其左侧,大的放在右侧,对左右两部分递归。 - 平均性能最优,划分最平衡,平均情况最接近最坏情况。
- 性能:
nlgn、nlgn、n^2^(最坏情况为划分不对称,如[1, 2, 3, 4],总是取本区间的最大值4/ 最小值1作为 pivot) - 空间:因为快排用递归(调用)实现, 每次函数调用中都用了常数的空间,因此空间复杂度 = 递归(工作栈的)深度
Θ(lgn);用双指针、后者覆盖前者的方式代替交换函数。 -
不稳定:待排序数组:
int a[] = {2, 2, 1, 3},在选择 pivot 时,把与基准元素相等的元素放在左边还是右边:- 若放在左边,选择第一个
2作为基准时,第二个2会被放在第一个2的右边,二者非原序(即不稳定); - 若放在右边,选择第二个
2作为基准时,第一个2会被放在第二个2的右边,二者非原序(即不稳定);
- 若放在左边,选择第一个
-
提高:
- 子序列规模较小时用直接插入;
- 划分尽量对称;

1 | |
3. 选择排序
3.1 简单选择排序
- 基本思想:一趟排序中,选择未排序序列
[i+1, n)中最小的元素,与未排序序列第一个元素交换,即添加在已排序序列的最后。与冒泡排序的区别是:已排序序列[0, i]在前面。 - 代码最简单直观。
- 性能:
n^2^、O(1)用于数据规模很小时,不占用额外的内存空间。 - 不稳定:
[2, 2, 1, 3],选择最小的1,与第一个2交换后,两个2的相对顺序改变了。
1 | |
3.2 堆排序
- 堆排序演示图;如
PriorityQueue即用堆排序实现; -
基本思想:
- 建大顶堆:将无序数组建立为一个二叉堆;从后向前遍历非叶节点
i(堆顶从下标0开始时,i = (n-1)/2 -> 0),按序逐个加入堆[i, n),即对所有以非叶节点i为根的子树向下调整堆; -
交换堆顶
a[0]和(堆底)末尾元素a[i = n-1->1];交换后,堆范围为[0, i), i = n-1->0,已排序序列为[i, n):- 弹出堆顶元素,作为最大值附在无序数组后(有序数组最前);
- 将末尾元素放至根结点,堆长度减一 。
-
维持剩余堆(
[0, i), i = n-1->0)的性质,向下调整新堆(即自顶向下堆化heapify,使该子树成为堆):- 交换父结点与左右子结点中的较大值 ;
- 交换后可能破坏子堆的结构,可递归也可迭代:沿交换后的子节点向下,交换较大的子节点,直到所有父结点
>=左右子节点(以该结点为根的子树成为堆)为止; - 时间复杂度为
lgn;
- 遍历无序数组(堆 ` i = n-1->0`),直到其中的所有元素都取出为止:
- 将堆顶的元素取出,作为次大值,与数组倒数第二位元素交换,并维持剩余堆的性质。
- 建大顶堆:将无序数组建立为一个二叉堆;从后向前遍历非叶节点
- 性能:
nlgn、O(1)。 -
不稳定:
- 在建堆时,关键字相同的两个记录,按序逐个加入并调整堆,相对位置不变,是稳定的;
- 但在堆顶与堆尾交换时,排在后面的元素可能被调整到前面,两个相等的记录(在序列中的)相对位置可能发生改变,是不稳定的。

1 | |
4. (2-路)归并排序
- 基本思想:将序列看作长度为
1的n个有序子序列,相邻子序列两两归并,合并为长度为2的有序子序列,直到合并成长度为n的1个有序序列。分治法的典型应用。 - 性能:
nlgn、O(n),需额外的内存空间;稳定。 -
算法步骤:
- 只有一个元素时直接返回,否则将序列分为两个子序列,并递归进行归并排序;
-
在递归后序位置进行归并,可使用返回的递归结果:
- 设定两个指针,分别指向两个已排序子序列的起始位置;
- 比较两指针所指向的元素,选择相对小的元素放入到归并结果,移动指针到下一位置;直到某一指针达到序列结尾;
- 将另一序列剩下的所有元素直接复制到合并序列后。
- 经典例题:
- 88.合并两个有序数组:拉链法,将双指针初始化在数组的尾部,从后向前进行合并,可避免占用多余空间;
- 剑指 Offer 25.合并两个排序的链表:归并法;链表双指针技巧;
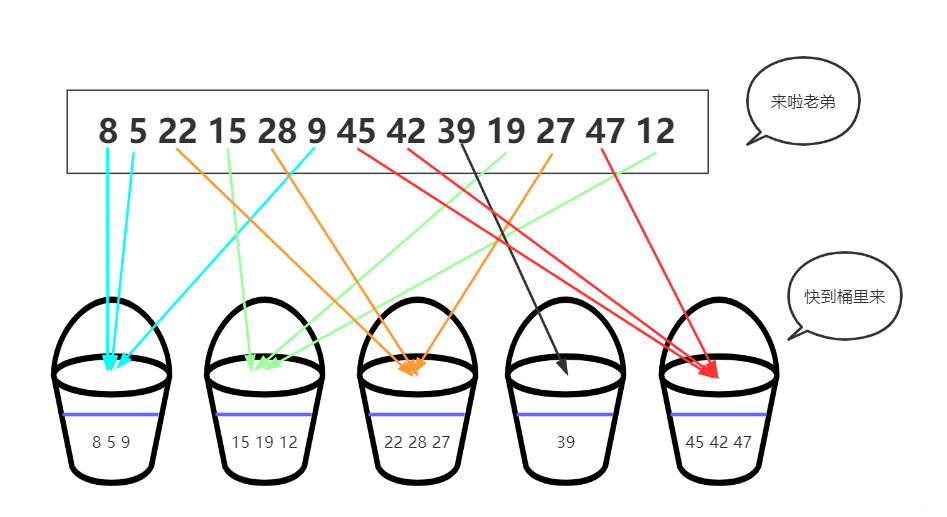
- 315.计算右侧小于当前元素的个数【】
1 | |
5. 非比较类的排序
5.1 计数排序
-
核心思想:
- 将输入的数据值
A[i]作为数组C的下标j,即第j个元素是待排序数组A中值等于j的元素的个数(类似于扑克插牌);根据C将A中的元素从后向前排到正确的位置。 - 适用于数据有确定范围、且范围较小的整数数组,可用在基数排序中用来排序数据范围更大的数组。
- 将输入的数据值
-
算法步骤:
- 找出最大和最小的元素;
- 创建新数组
C,长度是max+1或max-min+1,有助于节省新数组占用空间,默认值都为 0; - 遍历原数组
A,统计每个值为j的元素(j = nums[i]或j = nums[i] - min)出现的次数cnt,存入count[j] = cnt; - 求每个数出现次数
count的 前缀和:对所有的计数累加,新元素的值是该元素与前一个元素值的和,即当j>1时preCount[j] = count[j] + preCount[j-1],此处代码中preCount仍为count,表示原地求前缀和; - 创建结果数组
re,长度和原始数组A一致; - 从后向前(配合前缀和,不用每次都频繁计算当前元素前面有多少个元素,不用设置专门的变量存储和控制当前元素的剩余个数)遍历原始数组
A,利用前缀和,从右至左计算每个数的排名。反向填充结果数组:将nums[i]放在结果数组re中的preCount[j]-1位置,preCount[j] -= 1。

-
n + max;O(k),需额外的内存空间;稳定。
1 | |
5.2 基数排序
- 又称多关键字排序;
- 基本思想:(统一正整数长度),(从最低位开始)对元素中的每一位数字进行排序。最早用于解决卡片排序问题 。
-
算法步骤:
- 取数组中的最大值,计算其位数,作为迭代次数
N,如:数组中最大值为 1000,则N = 4; - 收集:从最低位开始取每位数字放入
radix数组; - (利用计数排序适用于小范围数的特点)对
radix进行计数排序; - 将
radix依次赋值给原数组; - 重复
2~4步骤N次。
- 取数组中的最大值,计算其位数,作为迭代次数
- 性能:
O(n x k),k为数组中元素的最大位数;需额外的内存空间; 稳定。

1 | |
5.3 桶排序
- 工作原理:(通过映射函数)将相同范围内的数据分到同一桶里,每个桶再分别排序(用其它排序算法或递归用桶排序)。
- 适用于待排序数据值域较大、但分布较均匀的情况。
-
桶排序是5.1计数排序的升级版。利用了函数的映射关系,高效与否的关键在于映射函数。为了更高效:
- 在额外空间充足的情况下,尽量增大桶的数量;
- 使用的映射函数能将输入的
N个数据均匀的分配到K个桶中;
-
算法步骤:
BucketSize:每个桶的容量;- 把数据依次映射到对应的桶里;
- 对每个非空桶排序,可用其它排序方法,也可递归用桶排序;
- 从非空桶里把排好序的数据,放回原来的序列中。
- 性能:
n+k、n^2^、n+k;O(k),需额外的内存空间; - 如果用稳定的内层排序(由于每块元素不多,一般用插入排序),且插入桶中时不改变元素间的相对顺序,此时稳定。

1 | |
6. 外部排序
外归并排序(External merge sort):读入一些能放在内存内的数据量,在内存中排序后输出为一个顺串(即内部数据有序的临时文件),处理完所有的数据后再进行归并。如,要对 900 MB 的数据进行排序,但机器上只有100 MB的可用内存时,按如下操作:
- 读入100 MB的数据至内存中,用某种内部排序(如快速排序、堆排序、归并排序等)在内存中完成排序。将排序完成的数据写入磁盘。
- 临时文件不用完全载入主存,读入每个临时文件(9个顺串)的前10 MB( = 100 MB / (9块 + 1))的数据放入内存中的输入缓冲区;剩余的10 MB 作为输出缓冲区。
- 用 PriorityQueue 优先队列实现最小堆(类似合并 K 个升序链表),执行九路归并算法,将结果输出到输出缓冲区。满了后将数据写出至目标文件,清空缓冲区。
- 一旦 9 个输入缓冲区中的一个变空,就从关联的文件再读入10M 数据,直到读完。
经典例题
- 第k大:一亿条数据选出其中1000个最大的;
- 外部排序 + 堆排序;
- 内存 1000M、文件 1G、10个出现次数最多的网址;
查找
顺序查找
二分查找
基本思想:减而治之(减治)思想,逐渐(减半)缩小问题规模。
1 | |
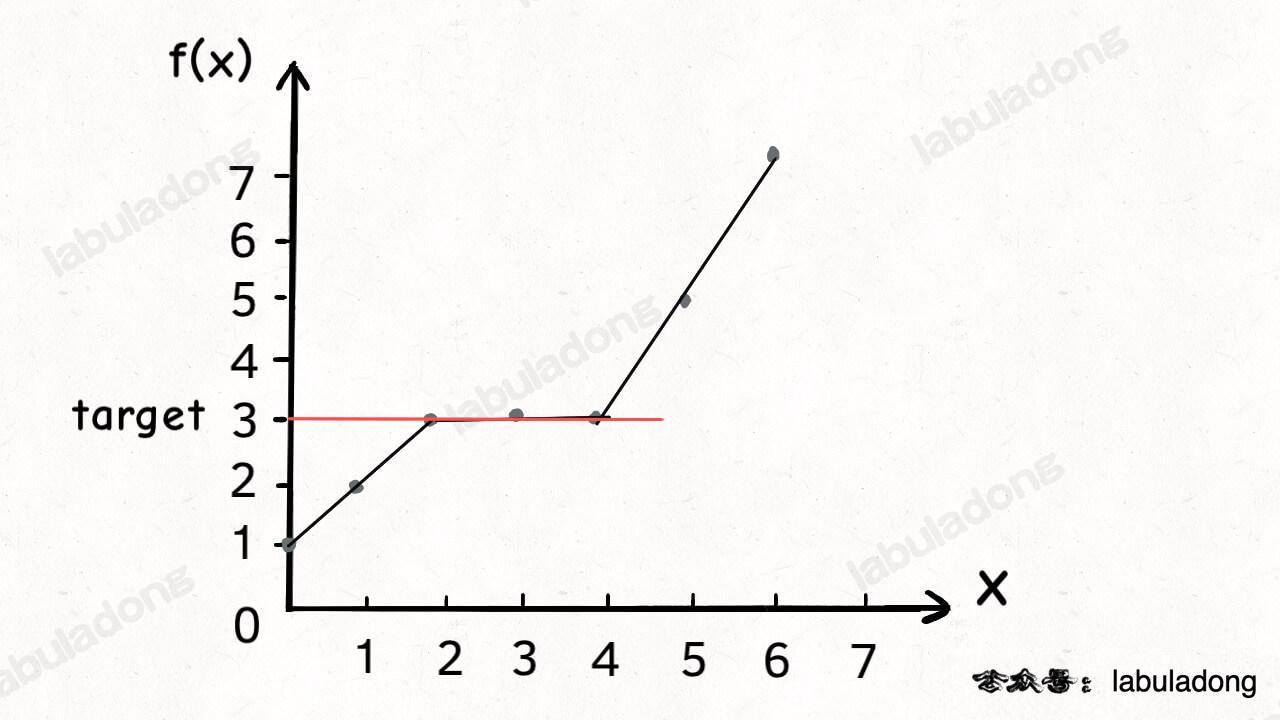
应用场景
- 有序数组中查找
target的下标;用于折半插入排序、二叉查找树等;- 计算满足约束条件
f(x) == target时自变量、下标x的取值范围(即搜索区间);
- 计算满足约束条件
- 找左、右边界的下标;
- 对时间复杂度要求
O(log n)、log(n);
经典例题
-
- 35.搜索插入位置:找左边界,找不到则插入:如
nums = [2,3,5,7]中搜索target = 4,搜索左边界的二分算法返回2;左边界也可理解为:【】nums中大于等于target的最小元素索引;target应在nums中插入的索引位置;nums中小于target的元素个数。
- 剑指 Offer 53-I.在排序数组中统计一个数字出现的次数:
repeatTime = lastPos - firstPos + 1;
- 35.搜索插入位置:找左边界,找不到则插入:如
-
- 中位数的定义:
- 当
m1 + m2是奇数时,是合并数组的第(m1 + m2)/2 + 1个元素; - 当
m1 + m2是偶数时,是第(m1 + m2)/2和第(m1 + m2)/2 + 1个元素的平均值(/2.0)。
- 当
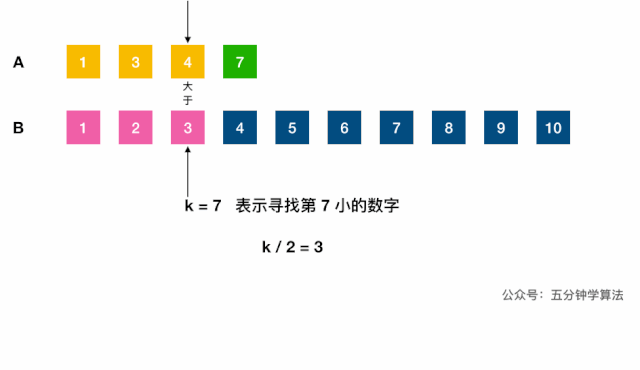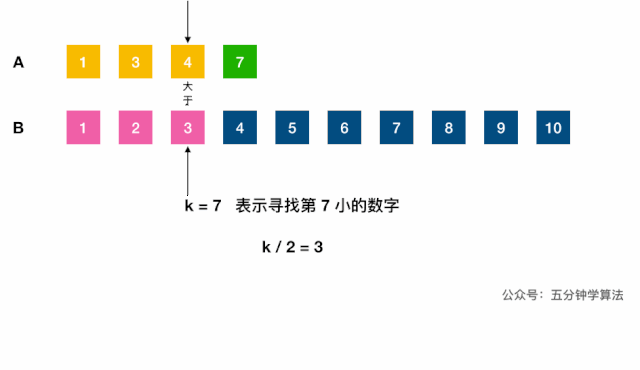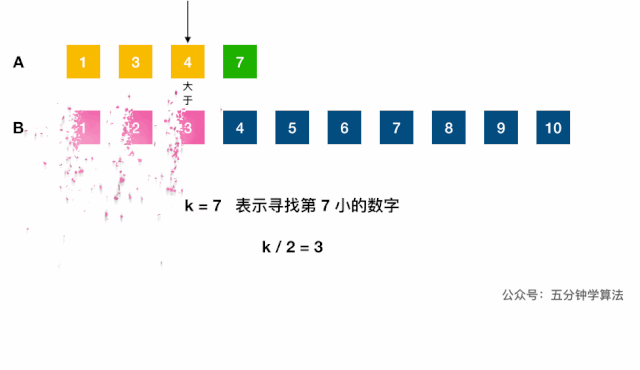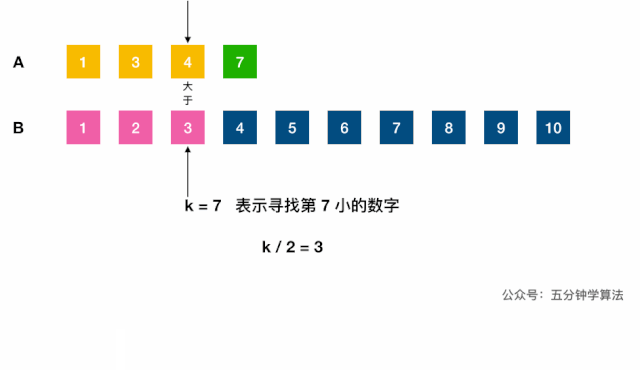
- 中位数对应的两下标之和是已知的
k = (m1 + m2)/2; 合并,根据奇偶计算,O(m, n);- 不合并,用双指针 + 二分查找的减治思想:
log(m1 + m2);- 调用(二分查找)虚拟合并的数组中第
k小的元素:- 分别找出两链表第
k/2大的数,对比,小的表明该数组的前k/2个数字都不是第k小数字,可舍弃; - 每次将
k自减(j-i) + 1长度,指向较小值的指针后移j + 1位,直到到达中位数的位置(k=1时,返回两数组较小的一个)。如果一个指针已到达数组末尾,则中位数一定在另一数组。
- 分别找出两链表第
- 调用(二分查找)虚拟合并的数组中第
- 链表中点
- 中位数的定义:
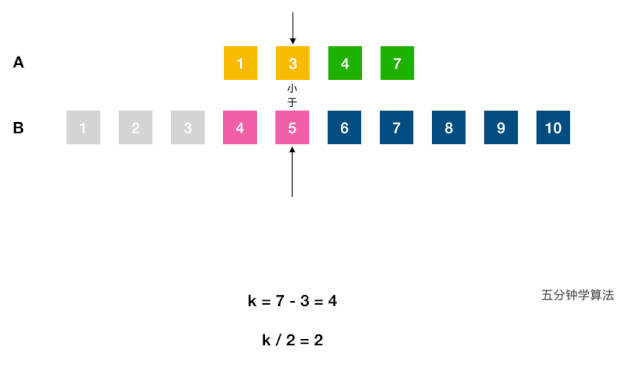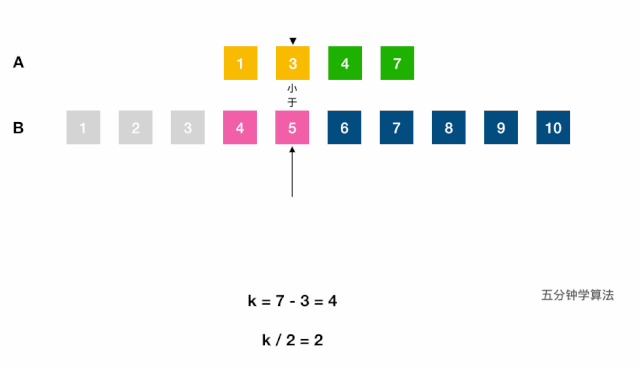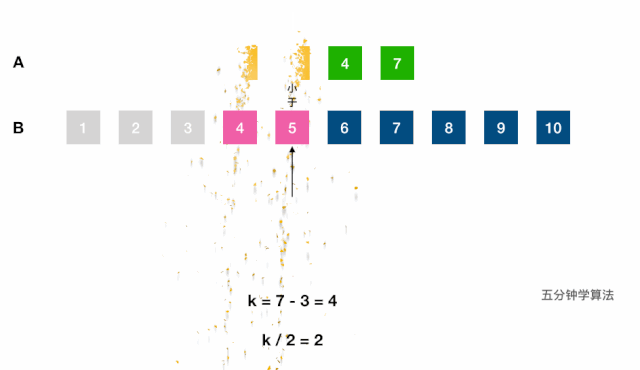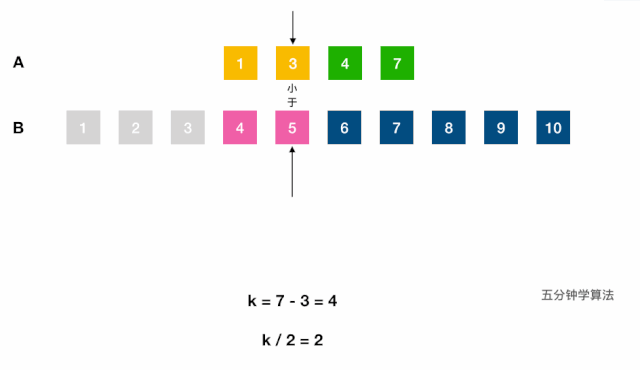
-
剑指 Offer 11.旋转数组的最小数字:二分查找左边界的变体,把数组最开始的若干个元素搬到末尾,
target> 前面的数字。[l, r)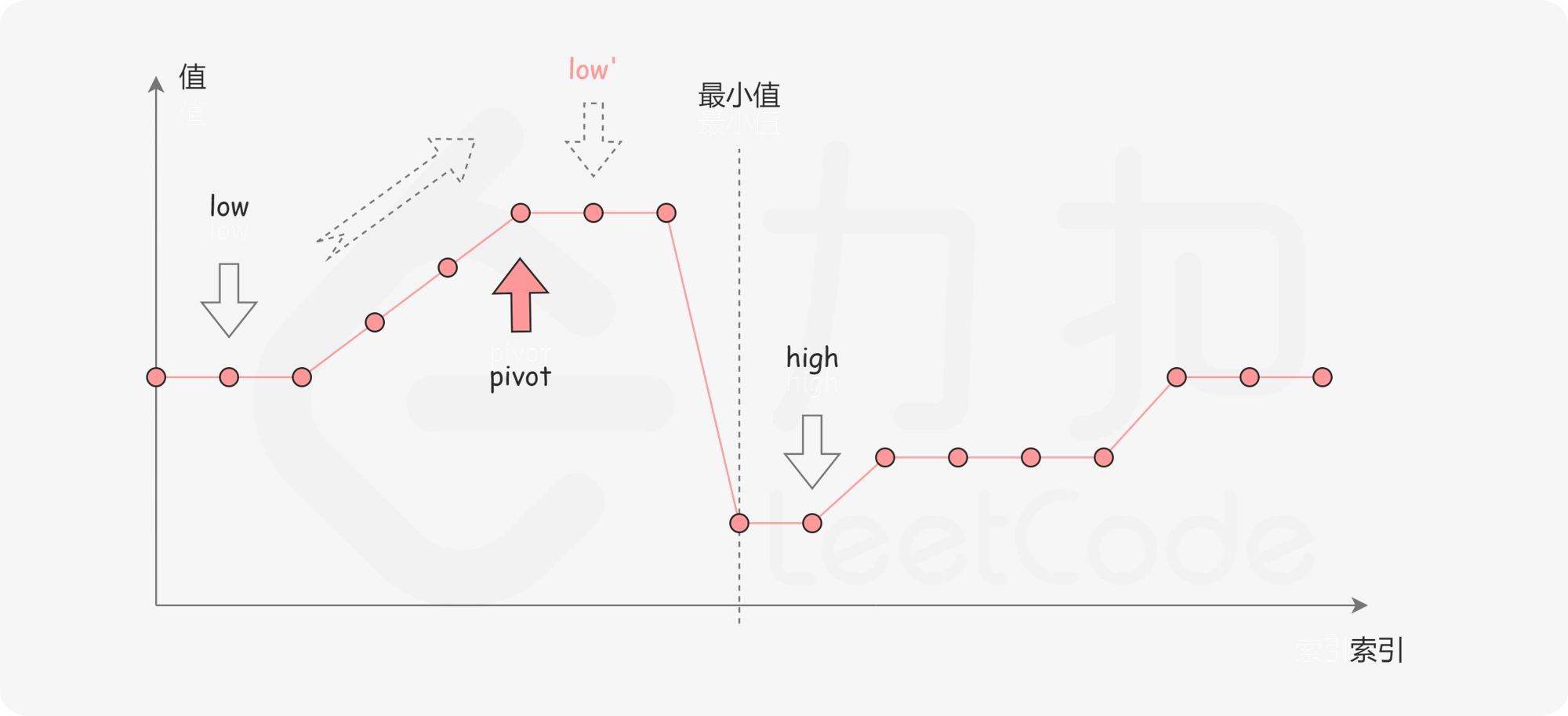
二分查找框架
常用
[begin,end)表示左闭右开,[left, right]、[from, to]表示左闭右闭,范围包括左右端点。
1 | |
B 树和 B+ 树
哈希表
字符串模式匹配
滑动窗口
见字符串中的滑动窗口
分治与递归
分治
分治(Divide and Conquer):问题分而治之;
- 分解 :将(复杂的)原问题分解为结构相同(相似、重叠)的子问题;
- 解决(触底):分解到某个容易求解的边界后,进行递归求解;
- 合并(回溯):将子问题的解合并成原问题的解。
递归
所有递归算法的本质上都是二叉树的遍历。
递归 VS 迭代:都是循环中的一种。
-
迭代:函数内某段代码实现循环,与普通循环的区别:将本次循环的输出作为下次循环的输入;循环代码中参与运算的变量同时是保存结果的变量,作为下一次循环的初始值。
- 向下调整堆,父子节点交换后,子节点成为新的父节点;
- 二分查找中用
mid更新查找区间[left, right]; - 动态规划,状态转移方程中通过做选择从当前状态转移到下一个状态;如,斐波那契数列;
-
递归(Recursion):重复调用函数自身实现循环。还指重复将问题分解为同类的子问题而解决问题的方法。
- 递推:把复杂问题的求解递推到简单问题的求解;
- 画出递归树,向下生长直到最简单情况,分析算法的复杂度、寻找算法低效的原因。
- 递归出口:必须有一个明确的递归结束条件;
- 回归:当获得最简单的情况后,逐层返回,依次得到复杂的解。
- 递推:把复杂问题的求解递推到简单问题的求解;
缺点是:递归层数过多时,会造成栈溢出。
打印递归树:

1 | |
经典例题
- 二叉树
- 菲波那切数列
- 阶乘
- 快速排序
- 二分查找
- 汉诺塔
BFS 框架
BFS 也是一种暴力穷举算法,必须掌握。本质就是二叉树的层序遍历,适合解决最短路径问题。
为什么常用 BFS 寻找最短路径?
为什么常用 DFS 寻找所有路径?
广度优先搜索常见场景
- 本质是在一幅「图或书」中,找到从起点
start到终点target的最短距离; - 遍历图(或树)
经典例题
- 最短路径 Dijkstra 算法模板:就是改造版 BFS 算法 + 类似 dp table 的数组。
- 752.打开转盘锁的最少步数
BFS 算法框架
1 | |
DFS 框架、回溯
分类的稍微有点粗糙了,没有细分出回溯/分治来
-
回溯算法:实际上就是多叉决策树的 DFS 遍历,关键是在前序和后序位置做一些操作。本质是:走不通就回头。回溯算法是一种纯粹的暴力穷举算法,必须掌握。
-
DFS 算法:本质上是一种暴力穷举算法,为图论中的概念。回溯算法是在遍历树枝,DFS 算法是在遍历节点。
常见场景
- 遍历图(或树);
- 基于树的 DFS:需要记住递归写前序、中序、后序遍历二叉树的模板;
- 二叉查找树(BST);
- 秒杀所有排列/组合/子集问题;
- 找出图或树中符合题目要求的全部方案;
- 图中(有向无向皆可)的符合某种特征(如最长)的路径及长度;
经典例题
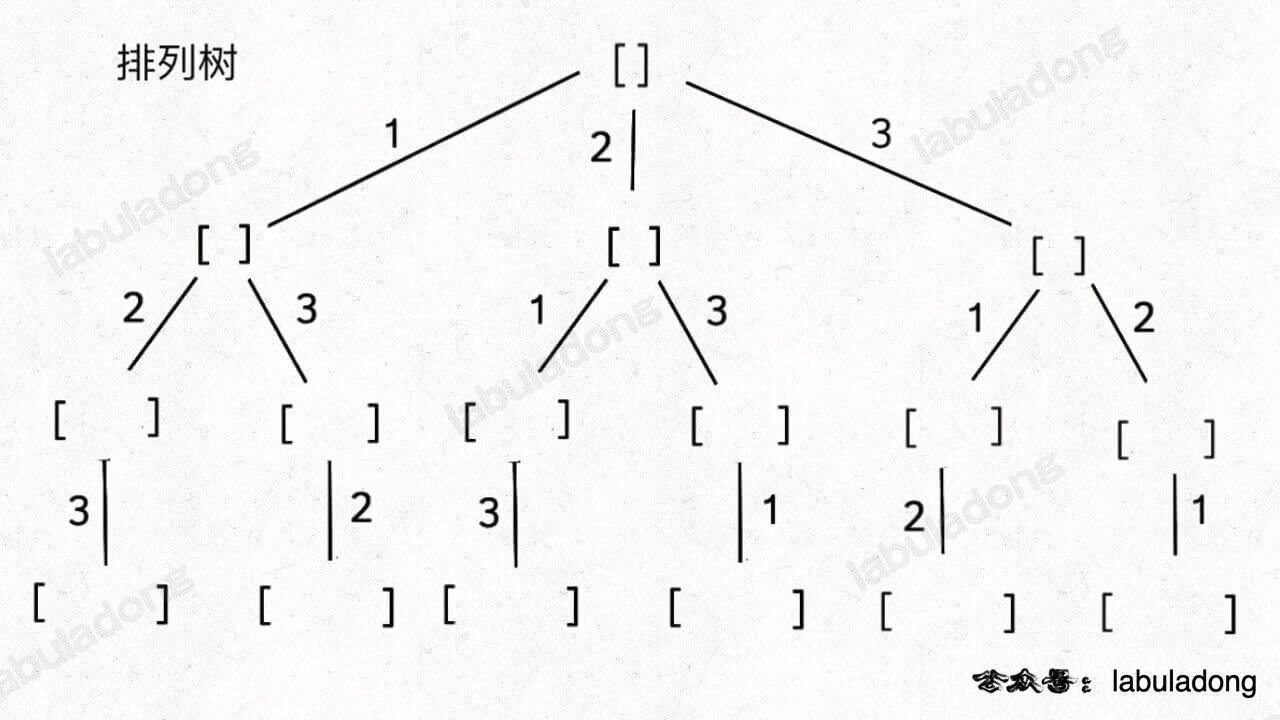
- 46.全排列(元素无重不可复选):回溯框架。
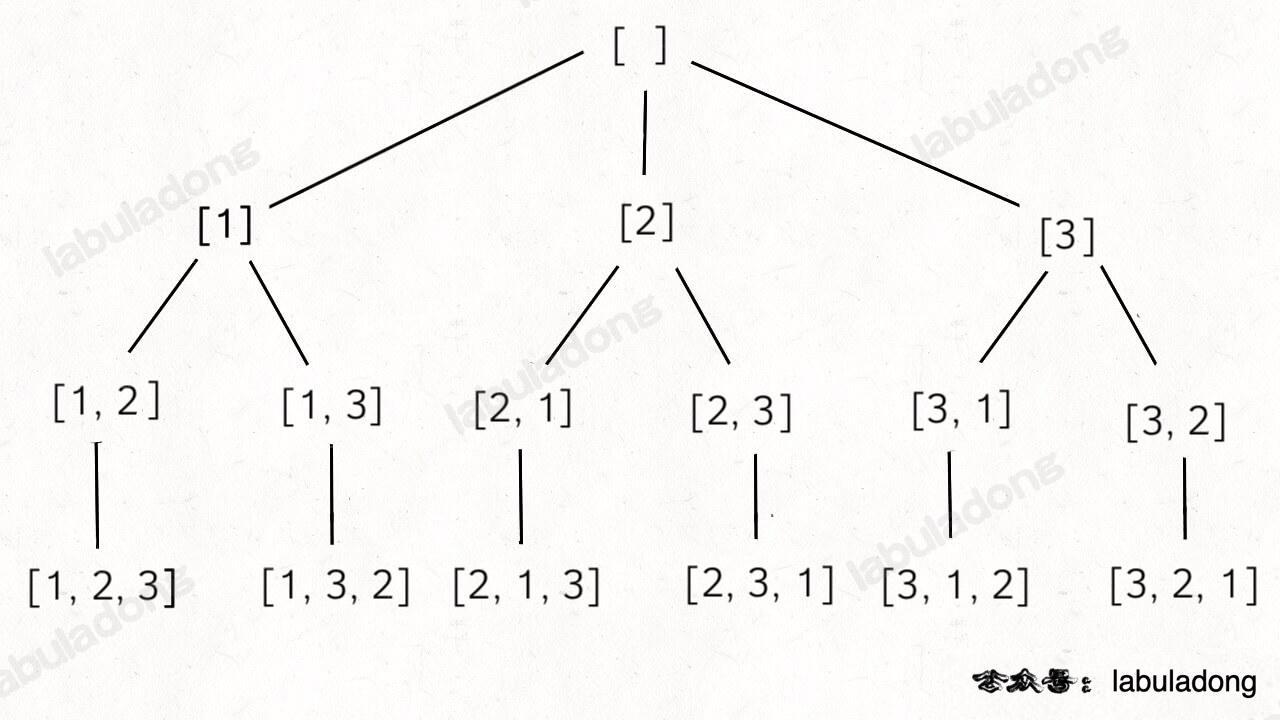
-
元素可重不可复选【】,即
nums中的元素可以存在重复,每个元素最多只能被使用一次。以组合为例,如果输入
nums = [2,5,2,1,2],和为 7 的组合应该有两种[2,2,2,1]和[5,2]。 -
元素无重可复选【】,即
nums中的元素都是唯一的,每个元素可以被使用若干次。以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该有两种 [2,2,3] 和 [7]。 -
- 通过保证元素间的相对顺序不变来防止出现重复的子集。
- 把根节点作为第 0 层,将每个节点和根节点间树枝上的元素作为该节点的值,那么第
n层的所有节点就是大小为n的所有子集 - 78.子集(元素无重不可复选)【】
组合/子集树:
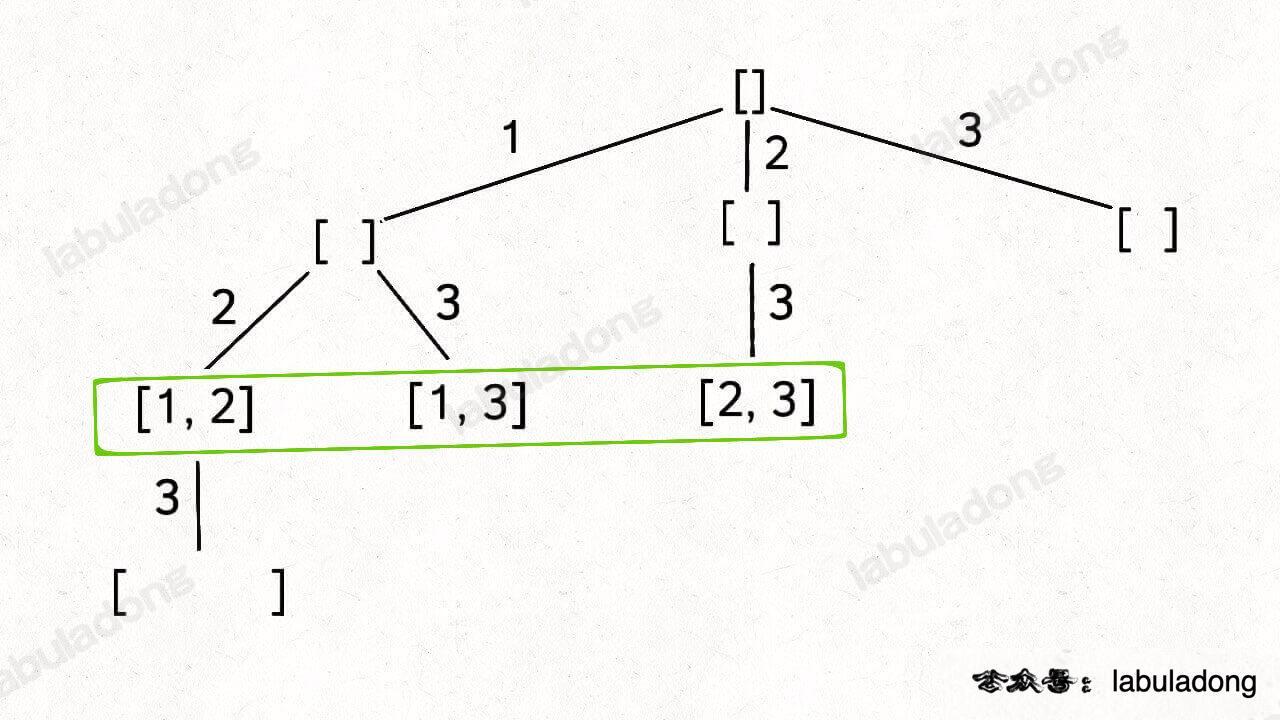
-
51.N 皇后:空间换时间【】
-
200.岛屿数量:将二维矩阵抽象成网状的图,每个节点和周围的四个节点连通,用 DFS 算法把遇到的岛屿「淹了」,避免维护
visited数组。
回溯算法经典例题
- 967.连续差相同的数字【】
- 491.递增子序列【】
- 980.不同路径 III【】
- 131.分割回文串【】
- 93.复原 IP 地址【】
- 17.电话号码的字母组合【】
- 79.单词搜索【】
回溯算法框架
站在回溯树的一个节点上,只需思考 3 个问题:
- 路径:已做出的选择;
- 选择列表:当前可做的选择;
- 结束条件:到达决策树底层,无法再做选择时。
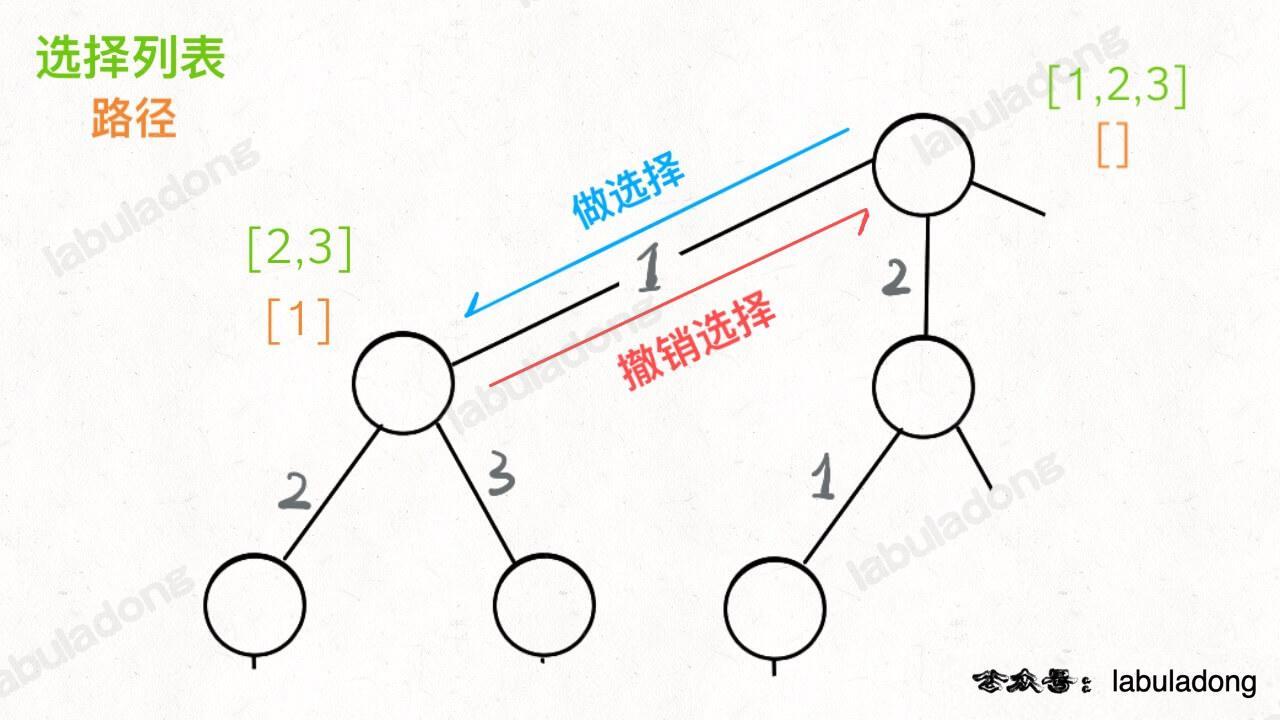
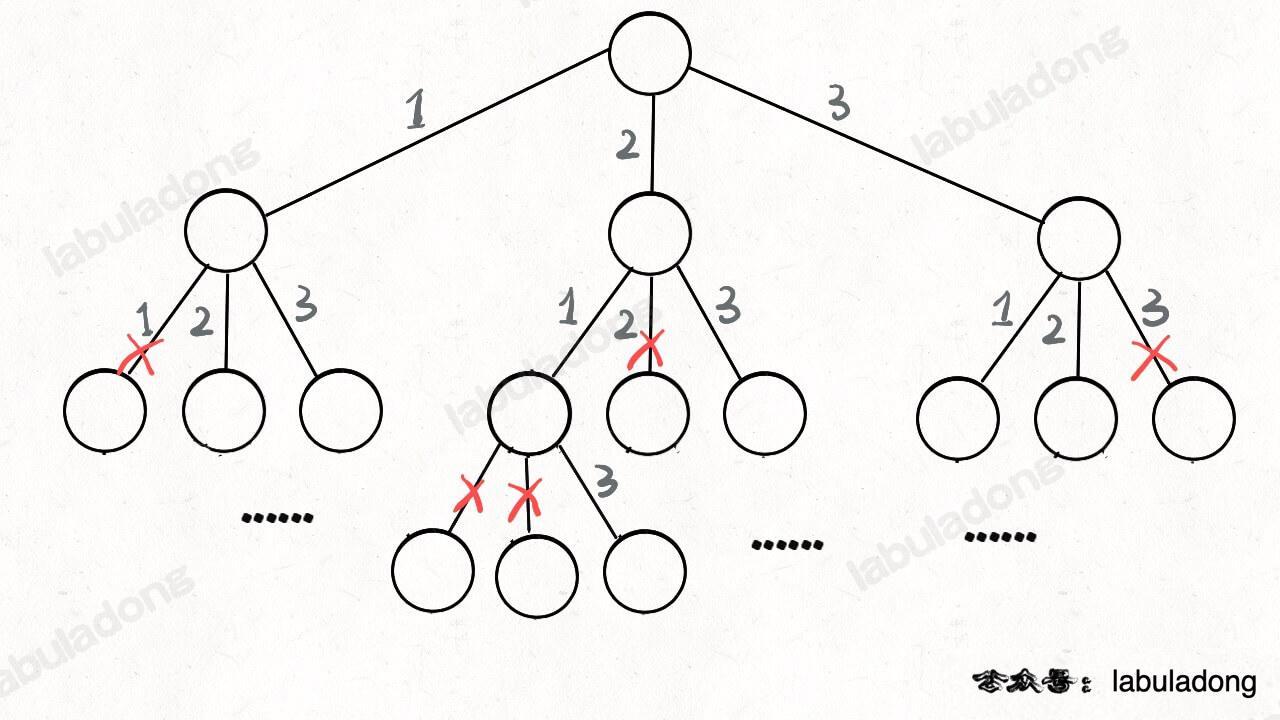
另见层序遍历二叉树
1 | |
贪心
贪心思路:每一步总是选取最优的操作,只看眼前,不考虑以后可能造成的影响。
每道题都不一样,没有通用解法。在有最优子结构的问题中尤为有效。
与动态规划的不同:在于对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,用于对当前进行选择,有回退功能。
- 134.加油站
- 数学图像解法:进入站点
i可加gas[i]的油(绿色),离开站点会损耗cost[i]的油(红色),那么可把站点和与其相连的路看做一个整体,将change[i] = gas[i] - cost[i]作为经过站点i的油量变化值(橙色)。 - 判断环形数组中是否能找到一个起点
start,使从此开始的累加和一直>= 0。累加和的最低点最有可能作为起点。若sum(gas[i] - cost[i]) < 0,即sum(gas[...]) < sum(cost[...]),总油量小于总消耗,无法环游所有站点,无解;否则原点即为所求。
- 数学图像解法:进入站点
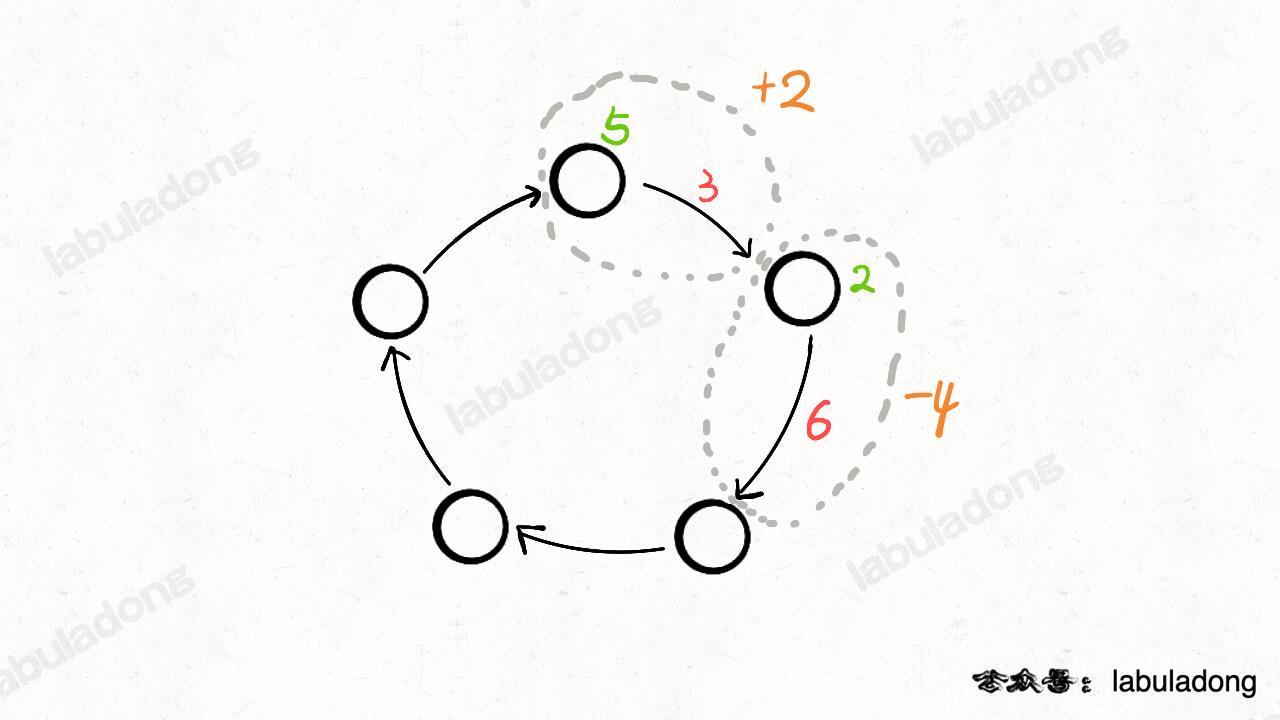
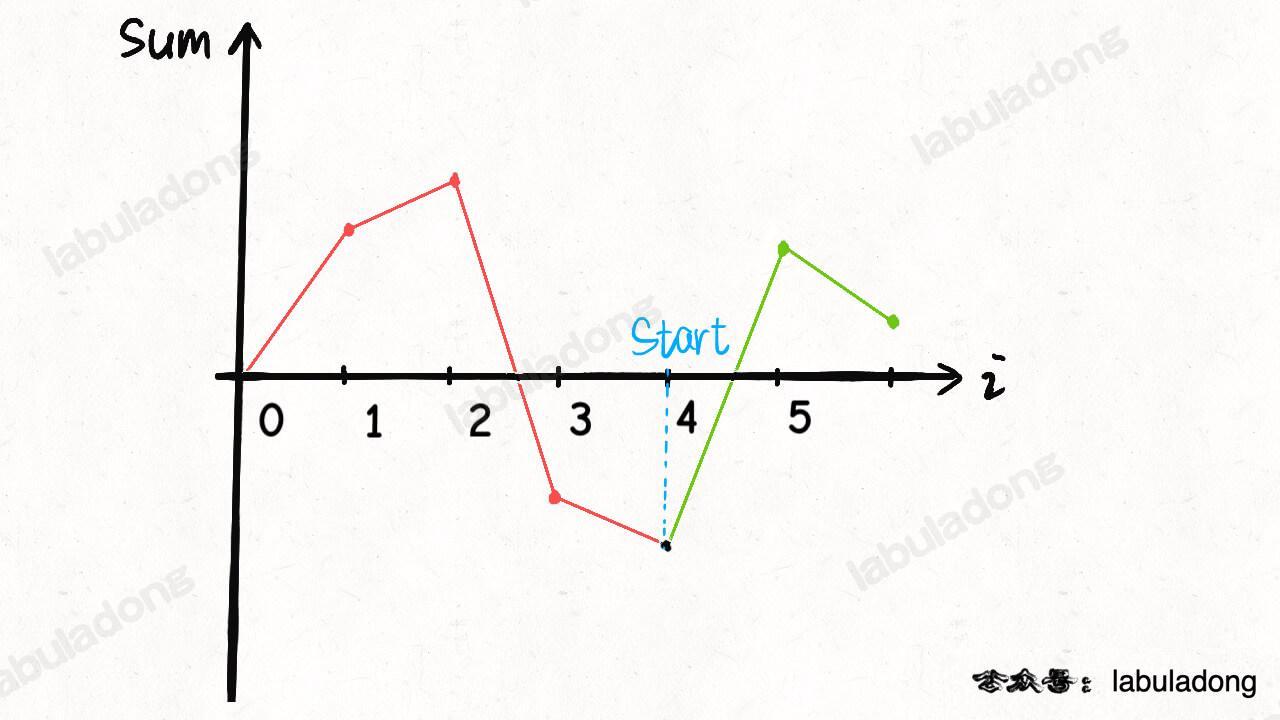
-
贪心解法:如果从i出发无法走到j,那么i及i, j间的所有站点都不可能作为起点。 - KMP 字符串匹配算法
- 最小生成树 Kruskal 算法
- 哈夫曼编码
动态规划
核心思想:如何聪明地穷举求最值。本质上是穷举「状态」,做「选择」找最优解。
动态规划的暴力穷举解法一般是递归形式,优化方法非常固定,要么是添加备忘录,要么是改写成迭代形式。
动态规划三要素
- 重复子问题:在计算的过程中,有一些问题会重复计算,必须记住结果;若没有重复子问题,可用「分治法」求解。
- 最优子结构:子问题间必须互相独立、可同时最优,不能互相影响。如要总分最高,则子问题为语文、数学等分别最高。如果语文、数学成绩互相制约、影响,不能同时达到最高,子问题并不独立,无法同时最优。
- 状态转移方程(暴力解):
- 明确 base case:直接从
最底下、最简单、问题规模最小、已知结果的,开始往上推,直到想要的答案。如f(1)和f(2)推出f(20)。 - 明确状态:记录解决问题到了哪一步,通常是原问题和子问题中随自变量变化的(题目中的)因变量,状态一般作为
dp数组的下标/key ;如目标金额n。 - 做选择:导致状态产生变化的行为,通过选择从一个状态转移到另一个状态。如,选择了一枚 1、2、5 元的硬币,从而目标金额
n减少了对应的 1、2、5 元。 - 定义
dp数组/函数的含义:一般 { key / 参数, value / 函数返回值 } = { 状态,题目要求计算的量/做选择的(最少)次数}。如 { 目标金额n,凑出n所需的最少硬币数量 / 至少需dp[n]枚硬币凑出}。 - 状态转移方程:对最后一步,可由已知的状态,通过选择所有情况(1、2、5元),转移到目标状态:
- 还差1元,dp[n] = dp[n - 1] + 1;
- 还差2元,dp[n] = dp[n - 2] + 1;
- 还差5元,dp[n] = dp[n - 5] + 1;
- 循环迭代:一般都脱离了递归,由循环迭代计算,自底向上进行递推求解。
- 优化递归树,消除重叠子问题:通过递归树找到被重复计算的子问题节点,寻找算法低效的原因。
- 通过剪枝,消除巨量冗余(重叠子问题),极大减少了子问题的个数。
- 分析递归算法的时间复杂度:子问题个数(即递归图中节点总数) X 解决一个子问题需要的时间。
- 降低时间复杂度:用空间换时间。
- 降低空间复杂度:如果每次状态转移只需 DP table 中的一部分,可尝试缩小 DP table 的大小,只记录必要的数据。
- 明确 base case:直接从
子序列
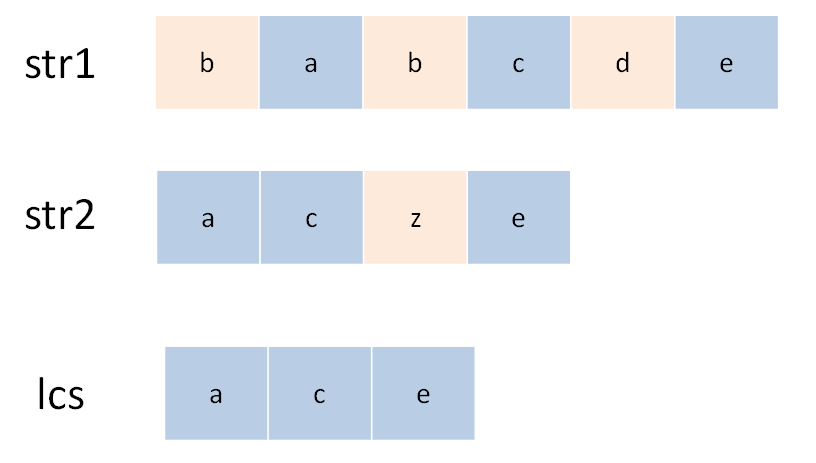
子序列 != 子串
子序列:不改变剩余字符顺序的情况下,删除某些字符或不删除任何字符形成的一个序列。另外定义见回文串。
-
双字符串动态规划(大多为二维)
-
- 定义:
dp[i][j]的含义是s1[0..i-1]和s2[0..j-1]的 LCS 长度; - 目标:
s1[0..m-1]和s2[0..n-1]的 lcs 长度,即dp[m][n]; base case:dp[0][..] = dp[..][0] = 0;- 剑指 Offer II 095.最长公共子序列【】
- 定义:
-
72.最小编辑距离:将
word1转成word2所使用的最少操作数 。【】- 定义
dp数组:dp[i-1][j-1]存储s1[0..i]和s2[0..j]的最小编辑距离。dp数组索引至少是 0,所以索引会偏移一位。



- 定义
-
-
516.最长回文子序列:区间 DP
与划分型 DP,在子串s[i,j]中,最长回文子序列的长度为dp[i][j];上一个可能的状态如下图: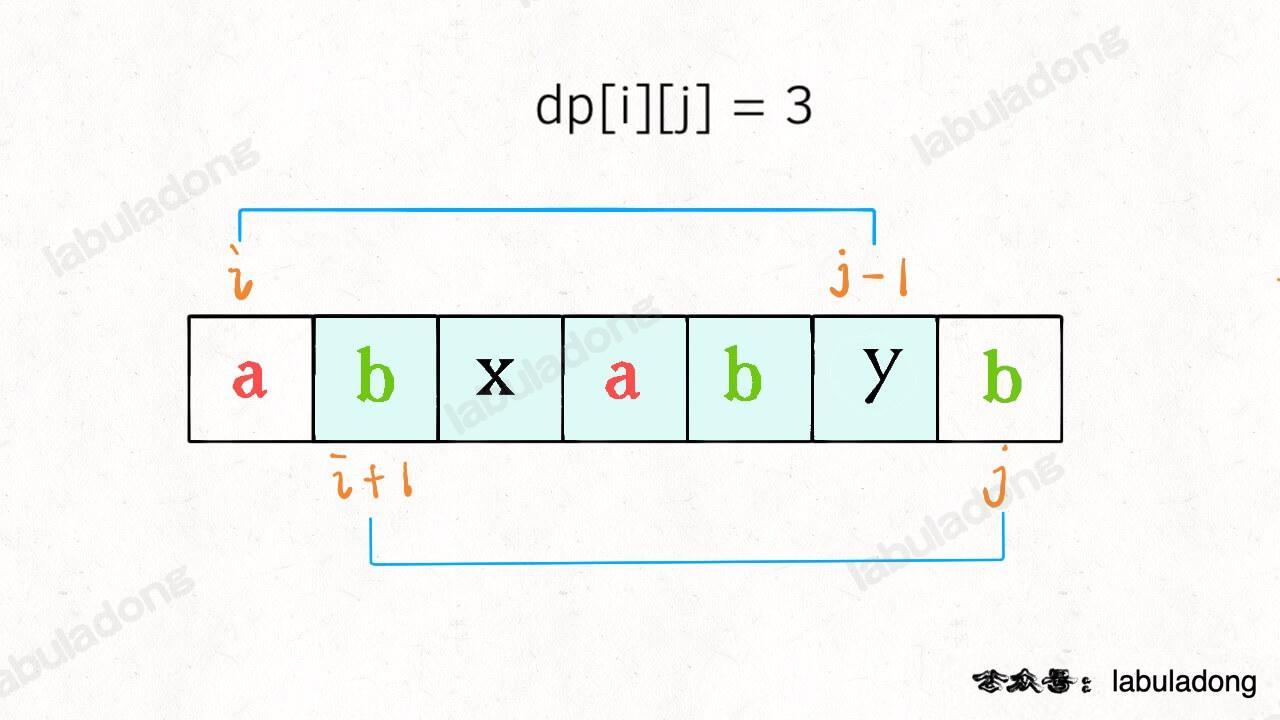
-
(一维)剑指 Offer 42.连续子数组的最大和、53.最大子数组和【】
- 300.最长递增子序列:
dp[i] = Math.max(dp[i], dp[j] + 1)
- 300.最长递增子序列:
经典例题
-
- 递归:简单,注意
0、1、2的情况,但大量的重复计算会导致内存溢出; 带「备忘录」、哈希表的递归算法,「自顶向下」进行递归求解。- 由动态规划的
dp数组通过消除递归得到迭代(递推)解法:(滚动数组)re0、re1交替前进,注意最值取模1e9+7、10,0000,0007防止溢出。
- 递归:简单,注意
-
剑指 Offer 10-II.青蛙跳台阶、爬楼梯问题:重复子问题,滚动数组。
- 状态:
- (最后一次)选择:还差跳 1 或 2 阶;
- dp 数组:{当前阶数,做的选择数、跳到 n 级台阶的方法个数};
- 状态转移方程:
dp[n] = dp[n-1]*1 + dp[n-2]*1; - 本质可理解为斐波那契数列:爬到第
n级台阶的方法个数等于爬到n-1的方法个数和爬到n-2的方法个数之和。
-
322.零钱兑换、剑指 Offer II 103. 最少的硬币数目:见 动态规划算法框架,最优子结构、如何列出状态转移方程【】
-
分割问题:416.分割等和子集:【】
-
先对集合求和,得出
sum,把问题转化为背包问题:背包容量为sum / 2和N个物品,每个物品的重量为nums[i]。 -
dp数组的定义:dp[i][j] = x表示,对于前i个物品,当前背包的容量为j时,若x为true,则说明可恰好将背包装满,若x为false,则说明不能恰好将背包装满。 -
0-1 背包问题:每个物体只有两种可能的状态(取与不取),对应二进制中的 0 和 1【重要】
-
-
-
各种玩小游戏
-
二维动态规划:121.买卖股票的最佳时机、剑指 Offer 63. 股票的最大利润:
dp[i][k][0 or 1]表示从第 i 天的这笔交易中获取的最大利润,0 和 1 代表是否持有股票,0 <= i < n, 1 <= k <= K,k 为交易次数(大 K 为交易数上限)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17特化到 k = 1 买入或卖出一次的情况: 状态转移方程:max(今天选择 rest, 今天选择 sell); 今天未持有股票,对于昨天来说,有两种可能,从中求最大利润: 1、昨天未持有,今天选择 rest 休息,仍未持有; 2、昨天持有,今天选择 sell,未持有股票。 dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]); 今天持有股票,有两种可能,从中求最大利润: 1、昨天就持有股票,今天选择 rest,今天仍持有股票; 2、昨天本没有持有,但今天选择 buy,持有了股票。 dp[i][1] = max(dp[i-1][1], -prices[i]); // 即前一天没有持有股票时、使dp[i-1][0]=0,今天选择买入则利润为-prices[i] base case: dp[0][0] = 0; dp[0][1] = -prices[i]; // Integer.MIN_VALUE;负数表示买入
动态规划算法框架
1 | |
位运算
- 136.只出现一次的数字:异或
^【】

- 268.丢失的数字 【】
- 异或法
- 求和法
算法应用
缓存淘汰算法
应用:
- Redis 缓存文档中的 #缓存淘汰策略、
- 操作系统中的 #内存管理 #页面置换算法。
总结:本质区别与选择
从本质上看,LRU 和 LFU 的核心差异是判断价值的维度不同:
- LRU 用最近是否被使用衡量价值,适合短期热点;
- LFU 用使用频率高低衡量价值,适合长期热点。
在 Redis 中,两者都做了性能优化(近似实现),选择时不用纠结 理论完美性,
- 先看业务访问模式:短期集中访问用 LRU,长期高频访问用 LFU。
- 如果实在不确定,不妨先试 LRU(实现更简单,兼容性更好),再根据监控数据调整。
LRU 基础算法
LRU(Least Recently Used)最近最少使用策略:优先删除、淘汰最久未使用的数据,即上次被访问时间距离现在最久的数据。
-
可以保证内存中的数据都是热点数据(经常被访问的数据),从而保证缓存命中率。
- 核心逻辑:最近没被用过的,下次也大概率用不上。
- 思路:保留最近使用的,淘汰最近最少使用的。
举例
例如:电脑桌面上放着常用的软件图标(微信、IDE),这些是最近常用的;而几个月没打开过的压缩工具,会被你拖到文件夹里。
缓存:
- 假设缓存容量只有 3,依次存入 A、B、C,此时缓存是 [A,B,C];
- 若此时访问 A(A 变成最近使用),缓存顺序变为
[B,C,A] - 若再存入D(缓存满了),需要淘汰最近最少使用的 B,最终缓存是 [C,A,D]
使用场景
LRU 适合短期高频场景,比如:
- 浏览器缓存:浏览器缓存网页时,会优先淘汰最近最少打开”的页面(比如一周没打开的网页,会被优先清理);
- Redis 默认内存淘汰策略:Redis 的
allkeys-lru和volatile-lru是基于 LRU 的(实际是 “近似 LRU”,性能更高),适合 “缓存访问具有短期局部性” 的场景(比如电商商品详情页,用户打开后短时间内可能再次刷新); - 本地缓存基础版:如果业务中没有突发大量一次性访问,用 LRU 实现本地缓存足够满足需求(比如用 LinkedHashMap 快速开发)。
优缺点
优点:
- 逻辑简单:只关注使用时间,实现成本低,容易理解
- 响应快:插入、删除、查询的时间复杂度可以做到 O (1)(用链表 + 哈希表实现)
- 贴合短期局部性:很多业务场景中,最近用的数据,确实接下来更可能用(比如刚打开的文档,接下来大概率会继续编辑)。
缺点:
- 突发访问误淘汰:如果突然有大量一次性数据访问,会把原本常用的缓存挤掉。
- 比如缓存容量 3,原本缓存 [A,B,C](A 是高频使用),突然连续访问 D、E、F,此时会淘汰 A、B、C,缓存变成 [D,E,F];但后续再访问 A 时,A 已经被淘汰,需要重新从数据库加载,导致缓存命中率骤降。
- 不考虑使用频率:如果 A 每天用 100 次,B 每天用 1 次,但 B 是 1 分钟前刚用,A 是 2 分钟前用,LRU 会优先淘汰 A,这显然不合理(高频使用的 A 不该被淘汰)。
实现方案
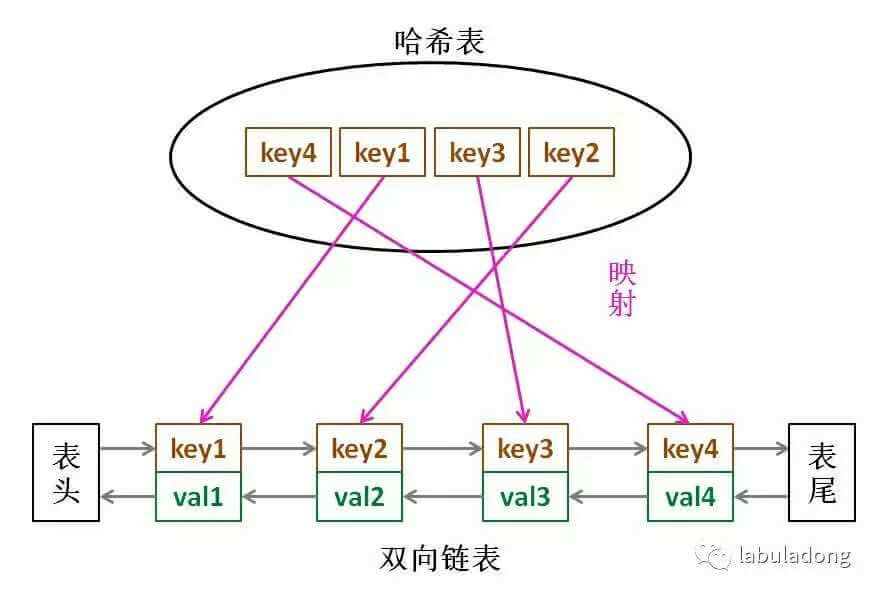
- 方案一、基于 双向链表 + HashMap 的实现
- 方案二、基于哈希链表
LinkedHashMap的实现(双向链表和哈希表的结合体)
淘汰尾部 or 头部?
基于双向链表 + HashMap
- 访问某个节点时,将其从原来的位置删除,并重新插入到链表头部。这样就能保证链表尾部存储的就是最近最久未使用的节点,(当节点数量大于缓存最大空间时)就淘汰链表尾部的节点。
- 为了使删除操作时间复杂度为 O(1),就不能采用遍历的方式找到某个节点。而是用 HashMap 存储着 Key 到节点的映射,通过 Key 就能以 O(1) 的时间得到节点,然后再以 O(1) 的时间将其从双向链表中删除。
LinkedHashMap本质是哈希表 + 双向链表,但如果想深入理解 LRU 的实现原理,建议自己手写一个。
- 核心是用哈希表保证 O (1) 查询,用双向链表保证 O (1) 插入、删除(维护访问顺序)。
- 适用于高并发场景和面试。
1 | |
基于哈希链表 LinkedHashMap
(双向链表和哈希表的结合体)
- Java 的
LinkedHashMap自带按访问顺序排序的功能,只需重写removeEldestEntry方法,就能实现 LRU 缓存。这是最简洁的实现方式,适合业务中不需要极致性能的场景,快速开发。 - 链表的有序性使元素维持插入顺序;每次默认从链表尾部添加元素,显然越靠尾部的元素就是最近使用的,越靠头部的元素就是最久未使用的。
- 双向链表:删除链表节点要得到前驱节点的指针,而双向链表支持直接查找前驱, O(1)。
- 哈希映射的快速访问能力、可在
O(1)时间访问链表的任意元素。定位到链表中的节点,从而取得对应val、插入和删除。 - 146.设计LRU 缓存的数据结构并实现 get()、put()
1 | |
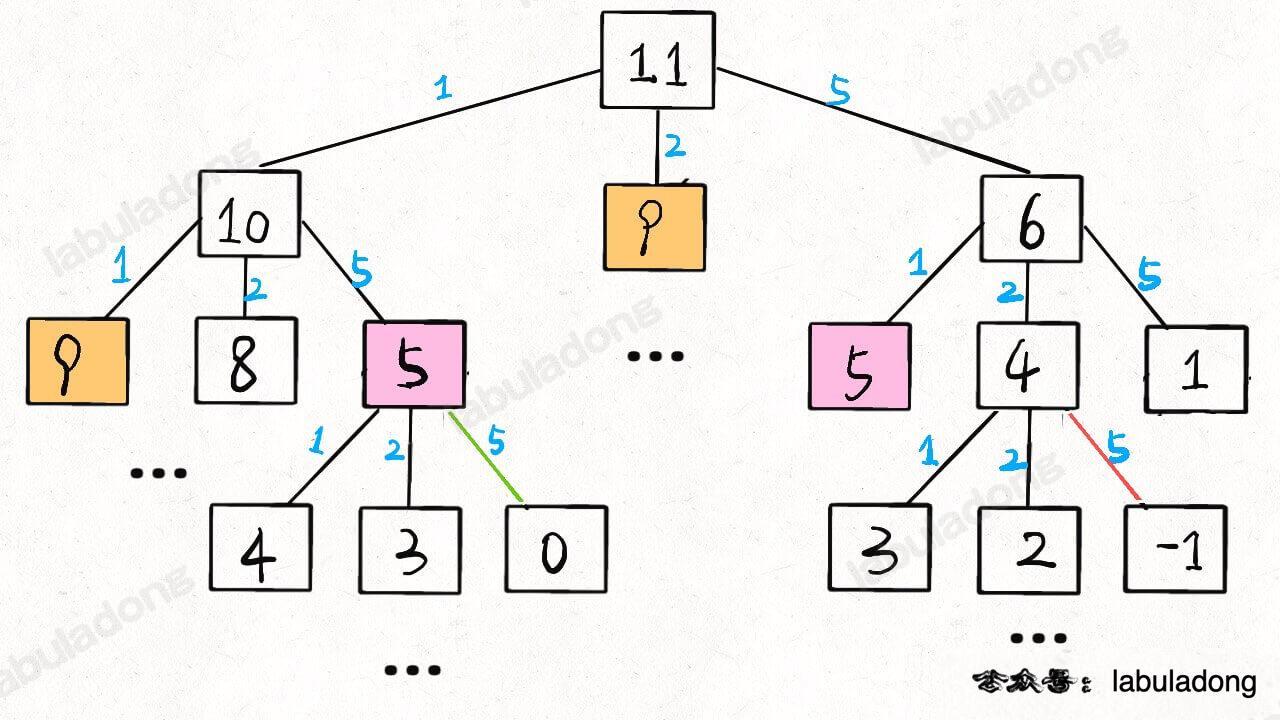
LFU 基础算法
LFU(Least Frequently Used)最不经常使用策略:优先淘汰一段时间内使用次数最少的数据。
- 核心逻辑和 LRU 完全不同:用得少的,下次也大概率用不上,它关注的是
使用频率,而不是使用时间。 - 按访问频率来淘汰,用一个
HashMap存储访问频率。 - 剑指 Offer II 031.最近最少使用缓存【】
举例
生活例子:
-
手机里的 APP,微信、抖音是高频使用的(每天打开几十次),而指南针是低频使用的(几个月打开一次)。
-
当手机内存不足时,系统会优先卸载指南针这类低频 APP,这就是 LFU 的思路。
缓存:
- 假设缓存容量 3,初始存入 A(使用 1 次)、B(使用 1 次)、C(使用 1 次),频率都是 1;
- 访问 A(A 频率变成 2),此时频率:A=2,B=1,C=1;
- 访问 A(A 频率变成 3),此时频率:A=3,B=1,C=1;
- 存入 D(缓存满了),需要淘汰 “频率最低” 的 B 或 C(若频率相同,淘汰 “最近最少使用” 的,即 LFU+LRU 结合),最终缓存是 A、C、D(频率分别为 3、1、1)。
优缺点
优点:
- 更贴合长期高频场景:能保留使用频率高的数据,即使它不是 最近使用的(比如 A 每天用 100 次,即使 10 分钟前没⽤,也不该被淘汰);
- 避免突发访问误淘汰:面对一次性突发访问(比如访问 D、E、F),因为这些数据的频率低,不会把高频的 A、B、C 挤掉,缓存命中率更稳定。
缺点:
- 实现复杂:需要维护使用频率,还需要处理频率相同的情况(通常结合 LRU),时间复杂度比 LRU 高(插入、删除约 O (log n));
- 冷启动问题:新存入的缓存频率低,容易被淘汰。比如一个新功能的接口,刚开始访问频率低,会被 LFU 优先淘汰,但其实后续会变成高频接口;
- 频率老化问题:一个数据过去高频,但现在不再使用(比如活动结束后的活动页面),它的高频率会一直占用缓存,导致新的高频数据无法进入。
实现 LFU
基于哈希表 + 优先级队列
LFU 的实现比 LRU 复杂,核心需要两个哈希表:
cache:key→Node(存储 value 和使用频率、最后使用时间);freqMap:频率→LinkedHashSet(存储该频率下的所有 key,LinkedHashSet 保证插入顺序,用于处理频率相同的情况);- 再用一个变量
minFreq记录当前最小频率,快速找到最该淘汰的 key。
- 再用一个变量
Redis 中的 LRU 和 LFU
Redis 作为缓存数据库,当内存达到内存maxmemory限制时,会触发内存淘汰策略,其中LRU和LFU是最常用的两种。
但 Redis 的实现并非 “严格版”,而是做了性能优化的 “近似版”, 这一点尤其需要注意。
Redis 的 LRU 实现
Redis 的 LRU 实现:近似 LRU(性能优先)
Redis 没有采用 “双向链表 + 哈希表” 的标准 LRU 实现,因为会增加内存开销和操作复杂度,而是用随机采样 + 时间戳实现近似 LRU:
- 核心原理:每个 key 在内存中记录
lru字段(最后一次访问的时间戳),当需要淘汰 key 时,Redis 会从所有候选 key 中随机采样 N 个(默认 5 个,可通过maxmemory-samples配置),然后淘汰这 N 个中lru值最小(最久未使用)的 key。 - 为什么近似:严格 LRU 需要维护全量 key 的访问顺序,在 Redis 高并发场景下会成为性能瓶颈;近似 LRU 通过控制采样数(N 越大越接近严格 LRU,但性能稍差),在 “命中率” 和 “性能” 之间做了平衡。
相关配置:
1 | |
Redis 的 LFU 实现
Redis 的 LFU 实现,结合频率与时间衰减。
Redis 4.0 引入了 LFU 策略,解决了标准 LFU 的频率老化问题,实现更贴合实际业务:
核心改进:
- 频率计数:用
lfu_count记录访问频率(但不是简单累加,而是用对数计数:访问次数越多,lfu_count增长越慢,避免数值过大); - 时间衰减:用
lfu_decay_time控制频率衰减(单位分钟),如果 key 在lfu_decay_time内没有被访问,lfu_count会随时间减少,避免过去高频但现在不用的 key 长期占用缓存。 - 淘汰逻辑:当需要淘汰时,同样随机采样 N 个 key,淘汰
lfu_count最小的(频率最低);若频率相同,淘汰最久未使用的(结合 LRU 逻辑)。
相关配置:
1 | |
核心区别
| 维度 | Redis LRU | Redis LFU |
|---|---|---|
| 判断依据 | 最后访问时间(越久未用越可能被淘汰) | 访问频率(频率越低越可能被淘汰,结合时间衰减) |
| 适用场景 | 短期局部性访问(如用户会话、临时数据) | 长期高频访问(如热点商品、基础配置) |
| 应对突发访问 | 弱(易被一次性访问挤掉常用 key) | 强(低频的突发访问 key 不会淘汰高频 key) |
| 冷启动友好度 | 较好(新 key 只要最近访问就不会被淘汰) | 需配置lfu-log-factor(避免新 key 因初始频率低被淘汰) |
| 内存 overhead | 低(只存时间戳) | 稍高(存频率和时间衰减信息) |
| 典型业务案例 | 新闻 APP 的最近浏览列表 | 电商首页的热销商品缓存 |
怎么选?
看业务访问模式。
选 LRU:如果你的缓存访问具有短期集中性(比如用户打开一个页面后,短时间内会频繁刷新,但过几天可能再也不看),比如:
- 会话缓存(用户登录后 1 小时内频繁操作,之后可能下线);
- 临时活动页面(活动期间访问集中,活动结束后很少访问)。
选 LFU:如果你的缓存访问具有 “长期高频性”(比如某些基础数据每天都被大量访问),比如:
- 商品类目、地区编码等基础配置数据;
- 首页 banner、热销榜单等高频访问数据。
- 排查技巧:可以先开启 Redis 的
INFO stats监控keyspace_hits(缓存命中)和keyspace_misses(缓存未命中),如果切换策略后keyspace_hits提升,说明更适合当前业务。
负载均衡算法
见负载均衡文档。
限流算法
见 限流、降级、熔断文档。